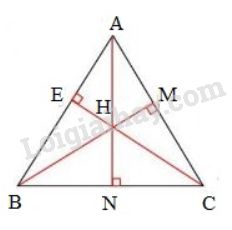
Bài 61 trang 83 SGK Toán 7 tập 2Cho tam giác ABC Đề bài Cho tam giác không vuông. Gọi là trực tâm của nó. a) Hãy chỉ ra các đường cao của tam giác Từ đó hãy chỉ ta trực tâm của tam giác đó. b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác Video hướng dẫn giải Phương pháp giải - Xem chi tiết Sử dụng dữ kiện là trực tâm tam giác , tức là giao điểm của ba đường cao của tam giác Lời giải chi tiết
Các đường thẳng lần lượt cắt cạnh đối tại a) có: nên là đường cao nên là đường cao nên là đường cao Mà là giao điểm của các đường thẳng nên là trực tâm của . b) có: nên là đường cao nên là đường cao nên là đường cao Mà là giao điểm của các đường nên là trực tâm của có: nên là đường cao nên là đường cao nên là đường cao Mà là giao điểm của các đường nên là trực tâm của .
|