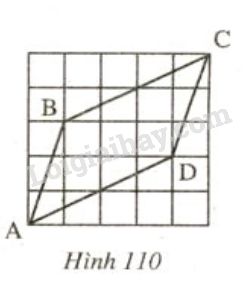
Bài 45 trang 125 SGK Toán 7 tập 1

Đề bài

Đố: Cho \(4\) đoạn thẳng \(AB,BC,CD,DA\) trên giấy kẻ ô vuông như ở hình 110. Hãy lập luận để giải thích:

a) \(AB=CD, BC=AD\);

b) \(AB//CD.\)

Lời giải chi tiết

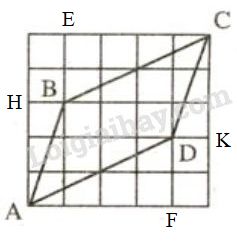
Xét \(∆AHB\) và \(∆ CKD\) có: 

+) \(HB=KD (= 1)\)

+) \(\widehat{ AHB}=\widehat{ CKD}=90^o\)

+) \(AH=CK(=3)\)

\( \Rightarrow  ∆ AHB = ∆  CKD\) (c.g.c)

\( \Rightarrow AB=CD \) (hai cạnh tương ứng)

Xét \(∆ CEB\) và \(∆ AFD\) có:

+) \(CE=AF(=4)\)

+) \(\widehat {CEB} = \widehat {AFD}\left( { = {{90}^o}} \right)\)

+) \(EB=FD(=2)\)

\( \Rightarrow  ∆ CEB = ∆ AFD\) (c.g.c)

\( \Rightarrow  BC = AD\) (hai cạnh tương ứng).

b) Xét \(∆ABD\) và \(∆CDB\)  có:

+) \(AB = CD\) (chứng minh trên)

+) \(BC = AD\) (chứng minh trên)

+) \(BD\) chung.

\( \Rightarrow ∆ABD = ∆CDB\) (c.c .c)

\( \Rightarrow \widehat{ ABD} = \widehat{ CDB}\) (hai góc tương ứng)

Mà \(\widehat{ ABD}\) và \(\widehat{ CDB}\) ở vị trí so le trong nên \(AB // CD.\) 

HocTot.Nam.Name.Vn