Bài 45 trang 11 SBT Hình học 12 Nâng caoGiải bài 45 trang 11 sách bài tập Hình học 12 Nâng cao. Cho khối chóp tứ giác đều S.ABCD... Đề bài Cho khối chóp tứ giác đều S.ABCD. Một mặt phẳng \(\left( \alpha \right)\) đi qua A, B và trung điểm M của cạnh SC. Tính tỉ số thể tích của hai phần khối chóp bị phân chia bởi mặt phẳng đó. Lời giải chi tiết
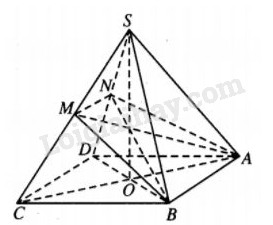
Kẻ \(MN//CD\left( {N \in SD} \right)\) thì hình thang \(ABMN\) là thiết diện của khối chóp khi cắt bởi \(mp\left( {ABM} \right)\). Ta có \(\eqalign{ & {{{V_{S.ANB}}} \over {{V_{S.ADB}}}} = {{SN} \over {SD}} = {1 \over 2}\cr& \Rightarrow {V_{S.ANB}} = {1 \over 2}{V_{S.ADB}} = {1 \over 4}{V_{S.ABCD}}. \cr & {{{V_{S.BMN}}} \over {{V_{S.CBD}}}} = {{SM} \over {SC}}.{{SN} \over {SD}} = {1 \over 2}.{1 \over 2} = {1 \over 4} \cr & \Rightarrow {V_{S.BMN}} = {1 \over 4}{V_{S.CBD}} = {1 \over 8}{V_{S.ABCD}}. \cr} \) Vậy \({V_{S.ABMN}} = {V_{S.ANB}} + {V_{S.BMN}} = {3 \over 8}{V_{S.ABCD}}\) Do đó : \({{{V_{S.ABMN}}} \over {{V_{ABMNCD}}}} = {3 \over 5}.\) HocTot.Nam.Name.Vn
|