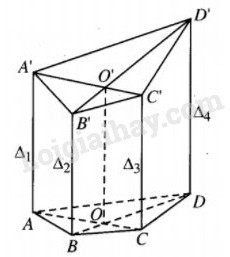
Bài 48 trang 11 SBT Hình học 12 Nâng caoGiải bài 48 trang 11 sách bài tập Hình học 12 Nâng cao. Bốn đường thẳng... Đề bài Bốn đường thẳng \({\Delta _1},{\Delta _2},{\Delta _3},{\Delta _4}\) đôi một song song và không có ba đường thẳng nào trên cùng một mặt phẳng. Một mặt phẳng \(\left( P \right)\) cắt chúng theo thứ tự tại A, B, C, D. Một mặt phẳng \(\left( {P'} \right)\) cắt chúng theo thứ tự A’, B’, C’, D’. Chứng minh hai khối tứ diện D’ABC và DA’B’C’ có thể tích bằng nhau. Lời giải chi tiết
Gọi \(O = AC \cap BD,O' = A'C' \cap B'D'.\) Do \(DD'//OO'\) nên dễ thấy \({{d\left( {D',\left( {ABC} \right)} \right)} \over {d\left( {O',\left( {ABC} \right)} \right)}} = {{DD'} \over {OO'}},{{d\left( {D,\left( {A'B'C'} \right)} \right)} \over {d\left( {O,\left( {A'B'C'} \right)} \right)}} = {{DD'} \over {OO'}}.\) Vậy : \(\left. \matrix{ {V_{D'.ABC}} = {{DD'} \over {OO'}}{V_{O'.ABC}} \hfill \cr {V_{D.A'B'C'}} = {{DD'} \over {OO'}}{V_{O.A'B'C'}} \hfill \cr} \right\}\;\;\;\;\;(1)\) Đặt \(h = d\left( {BB',\left( {ACC'A'} \right)} \right).\) Ta có \(h = d\left( {B,\left( {ACC'A'} \right)} \right)\) và \(\eqalign{ & {V_{O'.ABC}} = {V_{B.O'AC}} = {1 \over 3}h.{S_{O'AC}}\;\;\;\;\;(2) \cr & {V_{O.A'B'C'}} = {V_{B'.OA'C'}} = {1 \over 3}h.{S_{OA'C'}}\;\;\;(3) \cr} \) Đặt \(d = d\left( {AA',CC'} \right)\) thì \(\eqalign{ & {S_{O'AC}} = {S_{OA'C'}} = {1 \over 2}OO'.d\;\;\;\;(4) \cr & {S_{O'AC}} = {S_{AOO'}} + {S_{COO'}} \cr&\;\;\;\;\;\;\;\;\;\;= {1 \over 2}OO'\left( {d\left( {A,OO'} \right) + d\left( {C.OO'} \right)} \right) \cr&\;\;\;\;\;\;\;\;\;\;= {1 \over 2}OO'.d \cr} \) Tương tự \({S_{OA'C'}} = {1 \over 2}OO'.d\). Từ (2), (3), (4) suy ra \({V_{O'.ABC}} = {V_{O.A'B'C'}}\;\;\;\;(5)\) Từ (1) và (5) ta suy ra \({V_{D'.ABC}} = {V_{D.A'B'C'}}.\) HocTot.Nam.Name.Vn
|