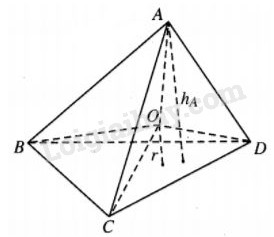
Bài 50 trang 11 SBT Hình học 12 Nâng caoGiải bài 50 trang 11 sách bài tập Hình học 12 Nâng cao. Cho tứ diện ABCD có điểm O ... Đề bài Cho tứ diện ABCD có điểm O nằm trong tứ diện và cách đều các mặt của tứ diện một khoảng cách r. Gọi \({h_A},{h_B},{h_C},{h_D}\) lần lượt là khoảng cách từ các điểm A, B, C, D đến các mặt đối diện. Chứng minh rằng : \({1 \over r} = {1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}.\) Lời giải chi tiết
Khối tứ diện ABCD được phân chia thành bốn khối tứ diện OBCD, OCAD, OABD, OABC. Từ đó dễ thấy rằng : \(\eqalign{ & {{{V_{O.BCD}}} \over {{V_{ABCD}}}} = {r \over {{h_A}}},{{{V_{O.CAD}}} \over {{V_{ABCD}}}} = {r \over {{h_B}}}, \cr & {{{V_{O.ABD}}} \over {{V_{ABCD}}}} = {r \over {{h_C}}},{{{V_{O.ABC}}} \over {{V_{ABCD}}}} = {r \over {{h_D}}}. \cr} \) Suy ra : \(\eqalign{ & {{{V_{O.BCD}} + {V_{O.CAD}} + {V_{O.ABD}} + {V_{O.ABC}}} \over {{V_{ABCD}}}}\cr& = r\left( {{1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}} \right) \cr & \Rightarrow {{{V_{ABCD}}} \over {{V_{ABCD}}}} = r\left( {{1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}} \right) \cr & \Rightarrow {1 \over r} = {1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}. \cr} \) HocTot.Nam.Name.Vn
|