Bài 53 trang 12 SBT Hình học 12 Nâng caoGiải bài 53 trang 12 sách bài tập Hình học 12 Nâng cao. Cho hình chóp tam giác S.ABC ...
Lựa chọn câu để xem lời giải nhanh hơn
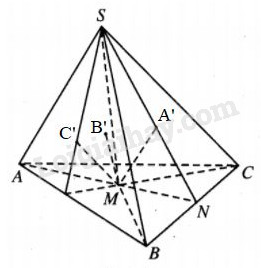
Cho hình chóp tam giác S.ABC và M là một điểm nằm trong tam giác ABC. Các đường thẳng qua M song song với SA, SB, SC lần lượt cắt các mặt \(\left( {BCS} \right),\left( {CAS} \right),\left( {ABS} \right)\) tại A’, B’, C’. Chứng minh rằng : LG a \({{{V_{M.BCS}}} \over {{V_{S.ABC}}}} = {{MA'} \over {SA}};\) Lời giải chi tiết: Gọi N là giao điểm của MA và BC. Khi đó S, A’, N thẳng hàng vì chúng cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SA,A'M} \right)\).
Gọi MM1 và AA1 là các đường vuông góc hạ từ M và A xuống \(mp\left( {SBC} \right)\) thì : \({{M{M_1}} \over {A{A_1}}} = {{MN} \over {AN}} = {{MA'} \over {SA}}.\) Vậy \({{{V_{M.BCS}}} \over {{V_{S.ABC}}}} = {{{V_{M.BCS}}} \over {{V_{A.BCS}}}} = {{{1 \over 3}{S_{BCS}}.M{M_1}} \over {{1 \over 3}{S_{BCS}}A{A_1}}} = {{M{M_1}} \over {A{A_1}}} = {{MA'} \over {SA}}\) LG b \({{MA'} \over {SA}} + {{MB'} \over {SB}} + {{MC'} \over {SC}}\) không đổi. Tìm tổng đó. Lời giải chi tiết: Chứng minh tương tự như câu a), ta có : \({{{V_{M.CAS}}} \over {{V_{S.ABC}}}} = {{MB'} \over {SB}},{{{V_{M.ABS}}} \over {{V_{S.ABC}}}} = {{MC'} \over {SC}}.\) Vậy : \({{MA'} \over {SA}} + {{MB'} \over {SB}} + {{MC'} \over {SC}} = {{{V_{M.BCS}} + {V_{M.CAS}} + {V_{M.ABS}}} \over {{V_{S.ABC}}}} \) \(= {{{V_{S.ABC}}} \over {{V_{S.ABC}}}} = 1.\) HocTot.Nam.Name.Vn
|