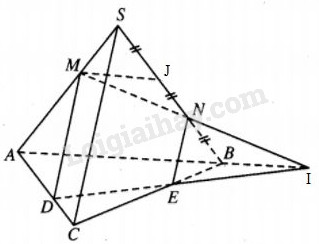
Bài 47 trang 11 SBT Hình học 12 Nâng caoGiải bài 47 trang 11 sách bài tập Hình học 12 Nâng cao. Cho điểm M trên cạnh SA, ... Đề bài Cho điểm M trên cạnh SA, điểm N trên cạnh SB của khối chóp tam giác S.ABC sao cho \({{SM} \over {MA}} = {1 \over 2},{{SN} \over {NB}} = 2.\) Mặt phẳng \(\left( \alpha \right)\) đi qua MN và song song với SC chia khối chóp thành hai phần. Tìm tỉ số thể tích hai phần đó. Lời giải chi tiết
Kéo dài MN cắt AB tại I. Kẻ MD song song với \(SC\left( {D \in AC} \right)\), DI cắt CB tại E. Vậy tứ giác MNED là thiết diện của khối chóp khi cắt bởi \(mp\left( \alpha \right)\). Ta có \(\eqalign{ & {{{V_{A.MDI}}} \over {{V_{A.SCB}}}} = {{AM} \over {AS}}.{{AD} \over {AC}}.{{AI} \over {AB}} \cr & = {2 \over 3}.{2 \over 3}.{4 \over 3} = {{16} \over {27}} \cr & \Rightarrow {V_{A.MDI}} = {{16} \over {27}}{V_{S.ABC}} \cr &(BI = MJ,MJ = {1 \over 3}AB\cr& \Rightarrow BI = {1 \over 3}AB,AI = {4 \over 3}AB ). \cr & {{{V_{I.BNE}}} \over {{V_{I.AMD}}}} = {{IB} \over {IA}}.{{IN} \over {IM}}.{{IE} \over {ID}} = {1 \over 4}.{1 \over 2}.{1 \over 2} = {1 \over {16}} \cr & \Rightarrow {V_{I.BNE}} = {1 \over {16}}{V_{A.MDI}} = {1 \over {27}}{V_{S.ABC}} \cr} \) Gọi \({V_1} = {V_{AMD.BNE}},{V_2}\) là phần còn lại thì \({V_1} = {V_{A.MDI}} - {V_{I.BNE}} = {{15} \over {27}}{V_{S.ABC}} = {5 \over 9}{V_{S.ABC}}\) Nên \({V_2} = {V_{S.ABC}} - {V_1} = {4 \over 9}{V_{S.ABC}}\) và \({{{V_1}} \over {{V_2}}} = {5 \over 4}\) HocTot.Nam.Name.Vn
|