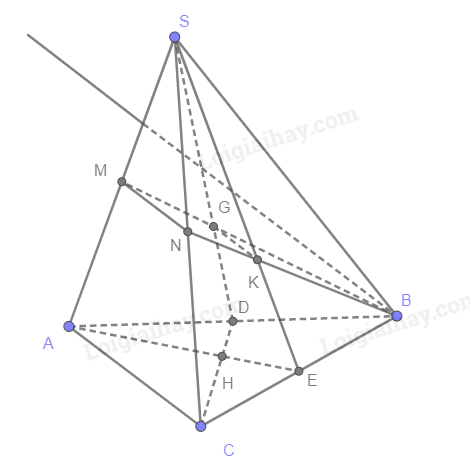
Bài 4.30 trang 124 SGK Toán 11 tập 1 - Cùng khám pháCho hình chóp S.ABC. Gọi G, K, H lần lượt là trọng tâm của các tam giác SAB, SBC, ABC. Đề bài Cho hình chóp S.ABC. Gọi G, K, H lần lượt là trọng tâm của các tam giác SAB, SBC, ABC. a) Chứng minh GK // (ABC). b) Tìm giao tuyến của (BGK) và (ABC). Phương pháp giải - Xem chi tiết a) Nếu đường thẳng d không nằm trong (P) song song với đường thẳng a nằm trong (P) thì d song song với (P). b) (P) và (Q) có điểm chung A và chứa lần lượt 2 đường thẳng a, b song song với nhau thì có giao tuyến d là đường thẳng đi qua A và song song với a, b. Lời giải chi tiết
a) Gọi M, N lần lượt là trung điểm của SA, SC Xét tam giác SAC có M, N lần lượt là trung điểm của SA, SC nên MN // AC (1) G, K lần lượt là trọng tâm của tam giác SAB, SBC nên \(\frac{{BG}}{{BM}} = \frac{{BK}}{{BN}} = \frac{2}{3}\). Suy ra GK // MN (2) Từ (1), (2) suy ra GK // AC. Mà AC nằm trong (ABC) Vậy GK // (ABC) b) (ABC) và (BGK) có chung điểm B, GK // AC nên giao tuyến của (ABC) và (BGK) là đường thẳng đi qua B, song song với GK, AC.  Chia sẻ Bình luận
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
|
