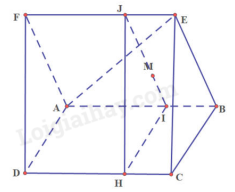
Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều

Đề bài

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.

a) Chứng minh rằng (AFD) // (BEC)

b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính \(\frac{{AN}}{{NC}}\)

Lời giải chi tiết

a) Ta có: AD // BC (ABCD là hình bình hành)

mà AD thuộc (AFD), BC thuộc (BEC)

nên (AFD) // (BEC)

b) Trong (ABEF), kẻ đường thẳng d qua M // AF

Ta có: d cắt AB tại I, d cắt EF tại J (1)

Trong (ABCD) có I thuộc  (P) mà (P) // (AFD)

Suy ra từ I kẻ IH // AD (2)

Từ (1) và (2) suy ra: (IJH) trùng (P) và // (AFD)

Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD)

Suy ra IH cắt AC tại N

Ta có các hình bình hành IBCH, IBEJ

Gọi O là trung điểm của AB

Ta có M là trọng tâm của tam giác ABE

Suy ra \(\frac{{MO}}{{ME}} = \frac{1}{2}\)

Ta có AB // CD suy ra AI // CH

Định lý Ta – let:\(\frac{{AN}}{{NC}} = \frac{{AI}}{{CH}}\)

Mà CH = IB (IBCH là hình bình hành)

Suy ra\(\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}}\)

Ta có: AB // EF nên OI // EJ

Do đó:\(\frac{{OI}}{{{\rm{EJ}}}} = \frac{{MO}}{{ME}} = \frac{1}{2}\)

Mà EJ = IB (IBEJ là hình bình hành)

Suy ra\(\frac{{OI}}{{IB}} = \frac{1}{2}\) hay\(IB = 2OI\)

Ta có\(\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}} = \frac{{AO + OI}}{{2OI}}\)

Mà OA = OB (O là trung điểm AB)

Nên \(\frac{{AN}}{{NC}} = \frac{{OB + OI}}{{2OI}} = 2\)

Do đó: \(\frac{{AN}}{{NC}} = 2\)