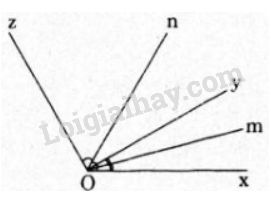
Bài 37 trang 87 SGK Toán 6 tập 2

Đề bài

Cho hai tia $Oy, Oz$ cùng nằm trên một nửa mặt phẳng có bờ chứa tia $Ox.$ Biết rằng $\widehat{xOy}=30^0$ , $\widehat{xOz}=120^0.$

a) Tính số đo góc $yOz.$ 

b) Vẽ tia phân giác $Om$ của $\widehat{xOy}$, tia phân giác $On$ của $\widehat{xOz}$. Tính số đo góc $mOn.$

Lời giải chi tiết

a)

Do hai tia $Oy, Oz$ cùng nằm trên một nửa mặt phẳng bờ chứa tia $Ox,$ mà: $\widehat {xOy} < \widehat {xOz}$ $(30^0<120^0)$ nên ta có tia $Oy$ nằm giữa hai tia $Ox, Oz,$ từ đó ta có:

$\widehat {xOy} + \widehat {yOz} = \widehat {xOz}$$\Rightarrow \widehat {yOz} = \widehat {xOz} - \widehat {xOy}$ 

$\widehat{yOz}=120^0-30^0=90^0$

b) Ta có tia $Om$ là tia phân giác của góc $xOy$ nên:

$\widehat {xOm} = \widehat {yOm} = \dfrac{{\widehat {xOy}}}{2}$$= \dfrac{{{{30}^0}}}{2} = {15^0}$

Ta có tia $On$ là tia phân giác của góc $xOz$ nên ta có:

$\widehat {xOn} = \widehat {nOz} = \dfrac{{\widehat {xOz}}}{2}$$= \dfrac{{{{120}^0}}}{2} = {60^0}$

Do hai tia $Om, On$ cùng nằm trên một nửa mặt phẳng bờ chứa tia $Ox,$ mà: $\widehat {xOm} < \widehat {xOn}$ $(15^0<60^0)$ nên ta có tia $Om$ nằm giữa hai tia $Ox, On,$ từ đó ta có:

$\widehat {xOm} + \widehat {mOn} = \widehat {xOn}$

$\Rightarrow \widehat {mOn} = \widehat {xOn} - \widehat {xOm}$$= {60^0} - {15^0} = {45^0}$

HocTot.Nam.Name.Vn