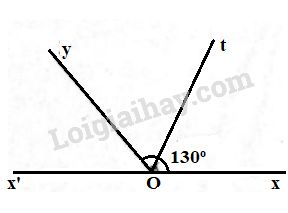
Bài 33 trang 87 SGK Toán 6 tập 2

Đề bài

Vẽ hai góc kề bù \(xOy, yOx',\) biết \(\widehat{xOy}=130^0\). Gọi \(Ot\) là tia phân giác của góc \(xOy.\) Tính số đo góc \(\widehat{x'Ot}\).

Lời giải chi tiết

Vì \(Ot\) là tia phân giác của góc \(xOy\) nên:

\(\widehat{xOt} = \widehat {tOy} \)\(= \dfrac{1}2\widehat{xOy}\) \(=\dfrac{130^{0}}2=65^0\)

Vì hai góc \(xOy, yOx'\) kề bù nên \( \widehat {xOy} + \widehat {yOx'} = {180^0}=\widehat {xOx'}\)

Trên cùng một nửa mặt phẳng có bờ là đường thẳng \(xx'\), ta có \(\widehat {xOt}<\widehat {xOx'} \,\,({65^0}<{180^0} )\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Ox'\) 

Do đó:  

\(\widehat {xOt} + \widehat {x'Ot} = \widehat {xOx'} \)
\(\Rightarrow \widehat {x'Ot} = \widehat {xOx'} - \widehat {xOt} \)\(= {180^0} - {65^0} = {115^0} \)

HocTot.Nam.Name.Vn