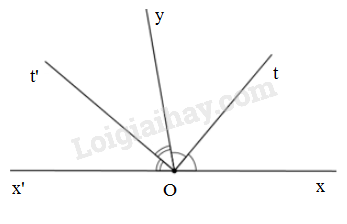
Bài 34 trang 87 SGK Toán 6 tập 2

Đề bài

Vẽ hai góc kề bù \(xOy\) và \(yOx',\) biết \(\widehat{xOy}=100^0\) . Gọi \(Ot\) là tia phân giác của góc \(xOy\) và \(Ot'\) là tia phân giác của góc \(x'Oy.\) Tính số đo các góc \(x'Ot, xOt', tOt'.\) 

Lời giải chi tiết

Hai góc \(xOy\) và \(x'Oy\) là hai góc kề bù nên \(\widehat{xOy}+\widehat{x'Oy}=180^0\) mà \(\widehat{xOy}=100^0\) nên \(\widehat{x'Oy}=180^0-\widehat{xOy}\)\(=180^0-100^0=80^0\) 

Vì \(Ot\) là tia phân giác của góc \(xOy\) nên \(\displaystyle \widehat {xOt} = \widehat {tOy} = {{\widehat {xOy}} \over 2}\)\( \displaystyle = {{{{100}^0}} \over 2} = {50^0}\)

Vì \(Ot'\) là tia phân giác của góc \(x'Oy\) nên \(\displaystyle \widehat {x'Ot'} = \widehat {t'Oy} \)\(\displaystyle = {{\widehat {x'Oy}} \over 2} = {{{{80}^0}} \over 2} = {40^0}\)

+ Góc \(x'Ot\) và góc \(xOt\) là hai góc kề bù nên \(\widehat {x'Ot} + \widehat {xOt}=180^0\)

Suy ra \(\widehat {x'Ot}=180^0-\widehat {xOt}=180^0-50^0=130^0\)

+ Góc \(xOt'\) và góc \(x'Ot'\) là hai góc kề bù nên \(\widehat {xOt'} + \widehat {x'Ot'}=180^0\)

Suy ra \(\widehat {xOt'}=180^0-\widehat {x'Ot'}=180^0-40^0=140^0\)

+ Vì tia \(Ot'\) nằm giữa hai tia \(Ox'\) và \(Oy,\) tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)

Lại có hai góc \(xOy\) và \(x'Oy\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ox'\)

Suy ra tia \(Oy\) nằm giữa hai tia \(Ot\) và \(Ot'\)

Do đó \(\widehat {yOt'} + \widehat {yOt}=\widehat {t'Ot}\)

Suy ra \(\widehat {t'Ot}=50^0+40^0=90^0\)

HocTot.Nam.Name.Vn