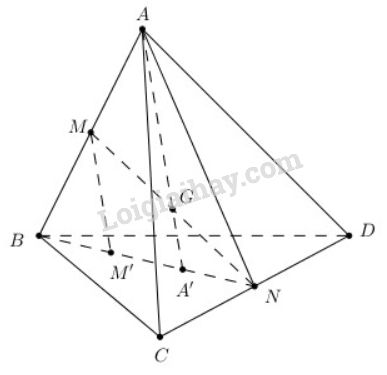
Bài 3 trang 60 SGK Hình học 11

Đề bài

Cho tứ diện \(ABCD\). Gọi \(M, N\) lần lượt là trung đểm của các cạnh \(AB, CD\) và \(G\) là trung điểm của đoạn \(MN\)

a) Tìm giao điểm \(A'\) của đường thẳng \(AG\) và mặt phẳng \((BCD)\)

b) Qua \(M\) kẻ đường thẳng \(Mx\) song song với \(AA'\) và \(Mx\) cắt \((BCD)\) tại \(M'\). Chứng minh \(B, M', A'\) thẳng hàng và \(BM' = M'A' = A'N\).

c) Chứng minh \(GA = 3 GA'\).

Lời giải chi tiết

a) Có: \(MN \subset \left( {ABN} \right)\)

\(\begin{array}{*{20}{l}}
{ \Rightarrow {\rm{ }}G \in \left( {ABN} \right)}\\
{ \Rightarrow {\rm{ }}AG \subset \left( {ABN} \right).}
\end{array}\)

Trong \((ABN)\): Gọi \(A'=AG  \cap BN\)

\( \Rightarrow A' \in BN \subset (BCD)\).

\( \Rightarrow A' \in (BCD) \Rightarrow  A' = AG \cap (BCD)\)

b) Ta có: \(\left\{ \begin{array}{l}MM'//AA'\\AA' \subset \left( {ABN} \right)\\M \in AB \subset \left( {ABN} \right)\end{array} \right. \) \(\Rightarrow MM' \subset \left( {ABN} \right)\)

Suy ra \(\left\{ \begin{array}{l}M' \in \left( {ABN} \right)\\M' \in \left( {BCD} \right)\end{array} \right.\)

\( \Rightarrow M' \in \left( {ABN} \right) \cap \left( {BCD} \right) = BN\).

Mà \(A'\) cũng thuộc \(BN\) nên \(M',A',B\) thẳng hàng (cùng nằm trên \(BN\)).

*) Xét tam giác \(NMM'\) có:

+) \(G\) là trung điểm của \(NM\).

+) \(GA'//MM'\)

\(\Rightarrow A'\) là trung điểm của \(NM'\)

Xét tam giác \(BAA'\) có:

+) \(M \) là trung điểm của \(AB\) 

+) \(MM'//AA'\)

\(\Rightarrow M'\) là trung điểm của \(BA'\)

Do đó: \(BM'=M'A'=A'N\).

c) Ta có \(\displaystyle MM'={1\over 2} AA'\)

\( \Rightarrow GA' = \frac{1}{2}MM' = \frac{1}{2}.\frac{1}{2}AA' = \frac{1}{4}AA' \)

\(\Rightarrow GA = AA' - GA' \) \(= AA' - \frac{1}{4}AA' = \frac{3}{4}AA'\)

\( \Rightarrow \dfrac{{GA'}}{{GA}} = \dfrac{{\dfrac{1}{4}AA'}}{{\dfrac{3}{4}AA'}} = \dfrac{1}{3} \) \(\Rightarrow GA = 3GA'\)

HocTot.Nam.Name.Vn