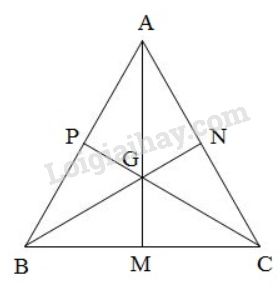
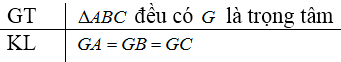Bài 29 trang 67 SGK Toán 7 tập 2Cho G là trọng tâm của tam giác đều ABC Đề bài Cho là trọng tâm của tam giác đều Chứng minh rằng:
Hướng dẫn: Áp dụng định lí ở bài tập Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng định lí ở bài tập : Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau. Lời giải chi tiết
Gọi lần lượt là trung điểm của các cạnh Vì là tam giác đều nên Xét có nên cân tại . (hai trung tuyến ứng với hai cạnh bên của tam giác cân thì bằng nhau theo định lí ở bài tập ) Mà (1) Xét có nên cân tại . (hai trung tuyến ứng với hai cạnh bên của tam giác cân thì bằng nhau theo định lí ở bài tập ) Mà (2) Từ (1) và (2) ta suy ra: (điều phải chứng minh).
|