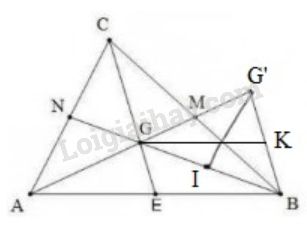
Bài 30 trang 67 SGK Toán 7 tập 2Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G′ sao cho G là trung điểm của AG′. a) So sánh các cạnh của tam giác BGG′ với các đường trung tuyến của tam giác ABC. b) So sánh các đường trung tuyến của tam giác BGG′ với các cạnh của tam giác ABC. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng tính chất đường trung tuyến của tam giác. Lời giải chi tiết
a) So sánh các cạnh của ∆BGG′ với các đường trung tuyến của ∆ABC. Gọi M,N,E lần lượt là trung điểm của BC,CA,AB. - Vì G là trọng tâm của ∆ABC⇒GA=23AM Mà GA=GG′ (G là trung điểm của AG′) ⇒GG′=23AM - Vì G là trọng tâm của ∆ABC ⇒GB=23BN - Ta có: GM=12AG (do G là trọng tâm) và AG=GG′ (giả thiết) ⇒GM=12GG′, do đó MG=MG′. Xét ∆GMC và ∆G′MB có: +) GM=MG′ (chứng minh trên) +) MB=MC (M là trung điểm của BC) +) ^GMC=^G′MB (hai góc đối đỉnh) Vậy ∆GMC=∆G′MB (c.g.c) ⇒BG′=CG (Hai cạnh tương ứng) Mà CG=23CE (G là trọng tâm tam giác ABC) ⇒BG′=23CE Vậy GG′=23AM,GB=23BN,G′B=23CE Hay mỗi cạnh của ∆BGG′ bằng 23 đường trung tuyến của ∆ABC. b) So sánh các đường trung tuyến của ∆BGG′ với các cạnh của ∆ABC. - Ta có: BM là đường trung tuyến ∆BGG′ Mà M là trung điểm của BC nên BM=12BC. Gọi I là trung điểm BG Vì IG=12BG (do I là trung điểm BG) GN=12BG (G là trọng tâm) ⇒IG=GN Xét ∆IGG′ và ∆NGA có: +) IG=GN (chứng minh trên) +) GG′=GA (giả thiết) +) ^IGG′=^NGA (hai góc đối đỉnh) Vậy ∆IGG′=∆NGA (c.g.c) ⇒IG′=AN (hai cạnh tương ứng) ⇒IG′=AC2 - Gọi K là trung điểm BG′ ⇒GK là trung tuyến của ∆BGG′ Vì GE=12GC (G là trọng tâm tam giác ABC) BG′=GC (chứng minh trên) ⇒GE=12BG′ Mà K là trung điểm BG′ ⇒KG′=EG Vì ∆GMC=∆G′MB (chứng minh trên) ⇒ ^GCM=^G′BM (hai góc tương ứng) Mà 2 góc này ở vị trí so le trong ⇒CE//BG′ ⇒ ^AGE=^AG′B (2 góc đồng vị) Xét ∆AGE và ∆GG′K có: +) EG=KG′ (chứng minh trên) +) AG=GG′ (giả thiết) +) ^AGE=^AG′B (chứng minh trên) Vậy ∆AGE=∆GG′K (c.g.c) ⇒AE=GK ( 2 cạnh tương ứng) Mà AE=12AB ⇒GK=12AB Vậy BM=12BC,G′I=12AC,GK=12AB Hay mỗi đường trung tuyến của ∆BGG′ bằng một nửa cạnh của tam giác ABC
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|