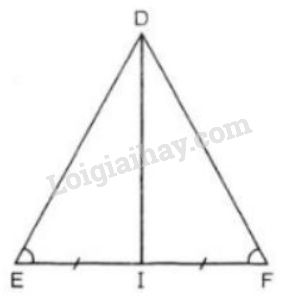
Bài 28 trang 67 SGK Toán 7 tập 2

Đề bài

Cho tam giác $DEF$ cân tại $D$ với đường trung tuyến $DI$.

a) Chứng minh $∆DEI  = ∆DFI.$

b) Các góc $DIE$ và góc $DIF$ là những góc gì?

c) Biết $DE = DF = 13\,cm,$ $EF = 10\,cm,$ hãy tính độ dài đường trung tuyến $DI.$

Lời giải chi tiết

a) Cách 1:

Xét $∆DEI$ và $∆DFI$ có:

+) $DE = DF$ (vì $∆DEF$ cân tại $D$)

+) $\widehat{DEI}=\widehat{DFI}$ (vì $∆DEF$ cân tại $D$)

+) $IE = IF$ ( vì $DI$ là trung tuyến)

Vậy $∆DEI  = ∆DFI$ (c.g.c)

Cách 2:

Xét $∆DEI$ và $∆DFI$ có:

+) $DI$ là cạnh chung

+) $DE = DF$ (vì $∆DEF$ cân tại $D$)

+) $IE = IF$ ( vì $DI$ là trung tuyến)

Vậy $∆DEI  = ∆DFI$ (c.c.c)

b) Vì  $∆DEI  = ∆DFI$ (theo câu a) nên $\widehat{DIE} =\widehat{DIF}$ ( 2 góc tương ứng)

Mà $\widehat{DIE} +\widehat{DIF} = 180^o$ ( hai góc kề bù)

$\Rightarrow$ $\widehat{DIE} =\widehat{DIF}$$=\dfrac{180^0}{2}= 90^o$ 

Vậy các góc $DIE$ và góc $DIF$ là những góc vuông.

c) $I$ là trung điểm của $EF$ nên $IE = IF =\dfrac{{EF}}{2} = \dfrac{{10}}{2}= 5\,cm.$

Áp dụng định lí Pytago vào $∆DEI$ vuông tại $I$ (do theo câu b góc $DIE$ vuông) ta có: 

$\eqalign{ & D{E^2} = D{I^2} + E{I^2} \cr & \Rightarrow D{I^2} = D{E^2}-E{I^2} \cr & \,\,\,\,\,\,\,\,D{I^2}\, = {13^2}-{5^2} = 144 \cr & \Rightarrow DI = 12\,\,cm \cr}$