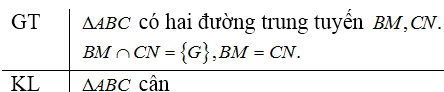Bài 27 trang 67 SGK Toán 7 tập 2

Đề bài

Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Lời giải chi tiết

Ta đưa về bài toán: Cho $∆ABC$ có hai đường trung tuyến $BM$ và $CN$ cắt nhau ở $G.$ Biết $BM=CN$, chứng minh tam giác $ABC$ là tam giác cân.

Vì $∆ABC$ có hai đường trung tuyến $BM$ và $CN$ cắt nhau ở $G$

$\Rightarrow$ $G$ là trọng tâm của tam giác $ABC$.

$\Rightarrow  GB = \dfrac{2}{3}BM$; $GC = \dfrac{2}{3}CN$. 

Mà $BM = CN$ (giả thiết) nên $GB = GC.$

Tam giác $GBC$ có $GB = GC$ nên $∆GBC$ cân tại $G$.

$\Rightarrow$ $\widehat{GCB} = \widehat{GBC}$ (Tính chất tam giác cân).

Xét $∆BCN$ và $∆CBM$ có: 

+) $BC$ là cạnh chung

+) $CN = BM$ (giả thiết)

+) $\widehat{GCB} = \widehat{GBC}$ (chứng minh trên)

Suy ra $∆BCN = ∆CBM$ (c.g.c)

 $\Rightarrow$ $\widehat{NBC} = \widehat{MCB}$ (hai góc tương ứng).

$\Rightarrow ∆ABC$ cân tại $A$ (tam giác có hai góc bằng nhau là tam giác cân) (điều phải chứng minh).

HocTot.Nam.Name.Vn