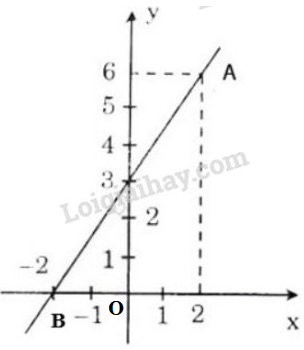
Bài 27 trang 58 SGK Toán 9 tập 1Cho hàm số bậc nhất y = ax + 3. Đề bài Cho hàm số bậc nhất \(y = ax + 3\) a) Xác định hệ số góc \(a\), biết rằng đồ thị của hàm số đi qua điểm \(A(2; 6)\). b) Vẽ đồ thị của hàm số. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Thay tọa độ điểm \(A\) vào công thức hàm số \(y=ax+3\) ta tìm được \(a\). b) Cách vẽ đồ thị hàm số \(y=ax+b,\ (a \ne 0)\): Đồ thị hàm số \(y=ax+b \, \, (a\neq 0)\) là đường thẳng: +) Cắt trục hoành tại điểm \(A(-\dfrac{b}{a}; \, 0).\) +) Cắt trục tung tại điểm \(B(0;b).\) Xác định tọa độ hai điểm \(A\) và \(B\) sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số \(y=ax+b \, \, (a\neq 0).\) Lời giải chi tiết a) \(y = ax + 3\) \((1)\) Theo giả thiết đồ thị hàm số đi qua điểm \(A(2; 6)\). Thay \(x=2,\ y=6\) vào \((1)\), ta được: \( 6=2.a+3 \Leftrightarrow 6-3=2a\) \(\Leftrightarrow 3=2a\) \(\Leftrightarrow a=\dfrac{3}{2}\) Vậy \(a=\dfrac{3}{2}\). b) Vẽ đồ thị hàm số: \(y=\dfrac{3}{2}x+3\) Cho \(x=2 \Rightarrow y=\dfrac{3}{2}.2+3=3 +3 =6 \Rightarrow A(2; 6)\). Cho \(y=0 \Rightarrow 0=\dfrac{3}{2}.x+3 \Rightarrow x=-2 \Rightarrow B(-2; 0)\). Đường thẳng đi qua hai điểm \(A(2;6)\) và \(B(-2;0)\) là đồ thị hàm số \(y=\dfrac{3}{2}x+3\). Đồ thị được vẽ như hình bên.
HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
