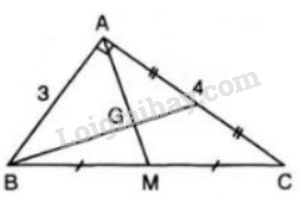
Bài 25 trang 67 SGK Toán 7 tập 2Biết rằng: Trong một tam giác vuông, Đề bài Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau: Cho tam giác vuông ABCABC có hai cạnh góc vuông AB=3cm,AC=4cm.AB=3cm,AC=4cm. Tính khoảng cách từ đỉnh AA tới trọng tâm GG của tam giác ABC.ABC. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng - Tính chất đường trung tuyến của tam giác và nhận xét trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền. - Định lí Pitago Lời giải chi tiết
Áp dụng định lí Pitago cho ∆ABCΔABC vuông tại AA ta có: BC2=AB2+AC2BC2=32+42=25 ⇒BC=5cm. Gọi M là trung điểm của BC ⇒ AM là trung tuyến ứng với cạnh huyền BC, do đó AM=12BC (1) (Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền). Vì G là trọng tâm của ∆ABC nên AG=23AM (2) Thay (1) vào (2) ta được: AG=23.12BC ⇒AG=13BC=13.5=53(cm). HocTot.Nam.Name.Vn
|