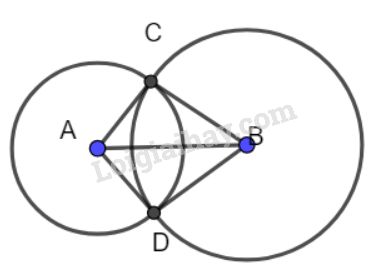
Bài 23 trang 116 SGK Toán 7 tập 1Cho đoạn thẳng AB dài 4cm Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm Đề bài Cho đoạn thẳng dài Vẽ đường tròn tâm bán kính và đường tròn tâm bán kính , chúng cắt nhau ở và , chứng minh rằng là tia phân giác của góc Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. Lời giải chi tiết
Vì là giao của đường tròn tâm và đường tròn tâm nên Vì là giao của đường tròn tâm và đường tròn tâm nên Do đó Xét và có: +) (chứng minh trên) +) (chứng minh trên) +) cạnh chung. Suy ra Suy ra = (hai góc tương ứng) Vậy là tia phân giác của góc . HocTot.Nam.Name.Vn
|