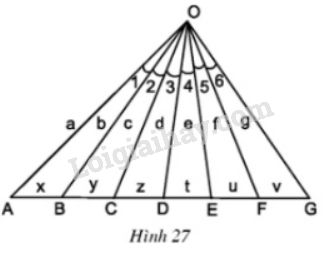
Bài 22 trang 68 SGK Toán 8 tập 2

Đề bài

Đố: Hình 27 cho biết có 6 góc bằng nhau:

\(\widehat{O_{1}} = \widehat {O_{2}} = \widehat {O_{3}} \)\(= \widehat {O_{4}} = \widehat {O_{5}} = \widehat {O_{6}}\). 

Kích thước các đoạn thẳng đã được ghi trên hình. Hãy thiết lập những tỉ lệ thức từ kích thước đã cho.

Lời giải chi tiết

\(OB\) là đường phân giác trong của \(∆OAC\) \( \Rightarrow \) \(\dfrac{x}{a} = \dfrac{y}{c}\)

\(OC\) là đường phân giác trong của \(∆OBD\) \(\Rightarrow \) \(\dfrac{y}{b} = \dfrac{z}{d}\)

\(OD\) là đường phân giác trong của \(∆OCE\) \( \Rightarrow \) \(\dfrac{z}{c}= \dfrac{t}{e}\)

\(OE\) là đường phân giác trong của \(∆ODF\) \( \Rightarrow \) \(\dfrac{t}{d} = \dfrac{u}{f}\)

\(OF\) là đường phân giác trong của \(∆OEG\) \( \Rightarrow \) \(\dfrac{u}{e} = \dfrac{v}{g}\)

\(OC\) là đường phân giác của  \(∆AOE\) \( \Rightarrow \) \(\dfrac{AC}{OA} = \dfrac{CE}{OE}\) hay \(\dfrac{x+ y}{a} = \dfrac{z + t}{e}\)

\(OE\) là đường phân giác của \(∆OCG\) \( \Rightarrow \) \(\dfrac{z + t}{c} =  \dfrac{u+v }{g}\)

\(OD\) làđường  phân giác của \(∆AOG\) \( \Rightarrow \) \(\dfrac{x+y+z }{a} = \dfrac{t+u+v }{g}\)

\(OD\) là đường phân giác của \(∆OBF\) \( \Rightarrow \) \(\dfrac{y+z}{b} = \dfrac{t + u}{f}\)

HocTot.Nam.Name.Vn