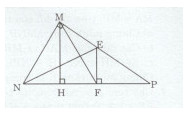
Bài 20 trang 170 Tài liệu dạy – học Toán 7 tập 1Giải bài tập Cho tam giác MNP vuông tại M. Tia phân giác của góc N cắt MP tại E. Đề bài Cho tam giác MNP vuông tại M. Tia phân giác của góc N cắt MP tại E. Kẻ EF⊥NP(F∈NP). a) Chứng minh rằng tam giác MNF cân. b) Kẻ MH⊥NP. Chứng minh rằng MF là phân giác của góc HME. Lời giải chi tiết a)Xét tam giác MNE vuông tại M và tam giác NEF vuông tại F ta có: ^MNE=^FNE (NE là tia phân giác của góc MNF) NE là cạnh chung. Do đó: ΔMNE=ΔFNE (cạnh huyền - góc nhọn) =>MN = NF => tam giác MNF cân tại N. b) Ta có: ME=EF(ΔMNE=ΔFNE) =>Tam giác MEF cân tại E ⇒^EMF=^EFM Mặt khác MH⊥NP(gt);EF⊥NP(gt) ⇒MH//EF⇒^HMF=^EFM (hai góc so le trong). Mà ^EMF=^EFM(cmt)⇒^HMF=^EMF Vậy MF là tia phân giác của góc HME. HocTot.Nam.Name.Vn
|