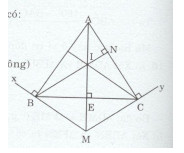
Bài 19 trang 170 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A. Kẻ \(Bx \bot AB\) và \(Cy \bot AC.\)  Gọi M là giao điểm của Bx và Cy.

a) Chứng minh rằng \(\Delta ABM = \Delta ACM.\)

b) Chứng minh rằng \(AM \bot BC.\)

c) Kẻ \(BN \bot C(N \in AC),\)   gọi I là giao điểm của BN với AM. Chứng minh rằng tam giác BIM cân.

d) Chứng minh rằng \(CI \bot AB.\)

Lời giải chi tiết

a)Xét tam giác ABM vuông tại B và tam giác ACM vuông tại C có:

AB = AC (tam giác ABC cân tại A)

AM là cạnh chung.

Do đó: \(\Delta ABM = \Delta ACM\)  (cạnh huyền - góc nhọn).

b) Xét tam giác BEM và CEM có:

EM là cạnh chung.

\(\eqalign{  & \widehat {EMB} = \widehat {EMC}(\Delta ABM = \Delta ACM)  \cr  & BM = CM(\Delta ABM = \Delta ACM) \cr} \)

Do đó: \(\Delta BEM = \Delta CEM(c.g.c) \Rightarrow \widehat {BEM} = \widehat {CEM}\)

Mà \(\widehat {BEM} + \widehat {CEM} = {180^0}\)   (hai góc kề bù).

Nên \(\widehat {BEM} + \widehat {BEM} = {180^0} \Rightarrow 2\widehat {BEM} = {180^0} \Rightarrow \widehat {BEM} = {90^0}\)

Vậy \(AM \bot BC.\)

c) Ta có: \(BN \bot AC(gt);MC \bot AC(gt)\)

\(\Rightarrow BN//MC \Rightarrow \widehat {BIM} = \widehat {IMC}\)   (hai góc so le trong).

Mà \(\widehat {IMC} = \widehat {BMI}(\Delta ABM = \Delta ACM) \Rightarrow \widehat {BIM} = \widehat {BMI}.\)

Do đó: Tam giác BIM cân tại B.

d) Xét tam giác BIM và CIM ta có:

BM = CM \((\Delta ABM = \Delta ACM)\)

IM là cạnh chung.

\(\widehat {BMI} = \widehat {CMI}(\Delta ABM = \Delta ACM)\)

Do đó: \(\Delta BIM = \Delta CIM(c.g.c) \Rightarrow \widehat {BIM} = \widehat {CIM}.\)

Mà \(\widehat {BIM} = \widehat {BMI}\)   (chứng minh trên). Do đó: \(\widehat {CIM} = \widehat {BMI}.\)

Mà hai góc CIM và BMI so le trong. Do đó CI // MB.

Mà \(MB \bot AB(gt) \Rightarrow CI \bot AB.\)

HocTot.Nam.Name.Vn