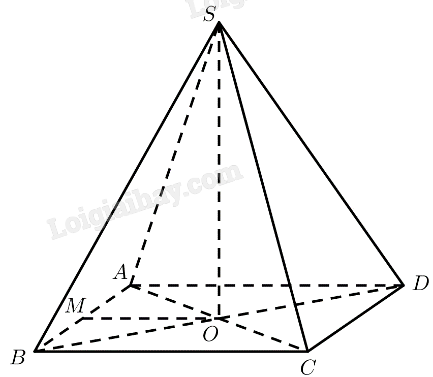
Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều

Đề bài

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, hai đường thẳng $AC$ và $BD$ cắt nhau tại $O$, $SO \bot \left( {ABCD} \right)$, tam giác $SAC$ là tam giác đều.

a) Tính số đo của góc giữa đường thẳng $SA$ và mặt phẳng $\left( {ABCD} \right)$.

b) Chứng minh rằng $AC \bot \left( {SBD} \right)$. Tính số đo của góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBD} \right)$.

c) Gọi $M$ là trung điểm của cạnh $AB$. Tính số đo của góc nhị diện $\left[ {M,SO,D} \right]$.

Lời giải chi tiết

a) $SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}$

Tam giác $SAC$ là tam giác đều $\Rightarrow \widehat {SAO} = {60^ \circ }$

$\Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }$

b) $ABC{\rm{D}}$ là hình vuông $\Rightarrow AC \bot B{\rm{D}}$

$SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC$

$\Rightarrow AC \bot \left( {SB{\rm{D}}} \right)$

$\Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }$

c) $SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO$

Vậy $\widehat {MO{\rm{D}}}$ là góc phẳng nhị diện của góc nhị diện $\left[ {M,SO,D} \right]$

$ABCD$ là hình vuông $\widehat {AOD} = {90^ \circ }$

$\Delta AMO$ vuông cân tại $M \Rightarrow \widehat {AOM} = {45^ \circ }$

$\Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }$

Vậy số đo của góc nhị diện $\left[ {M,SO,D} \right]$ bằng ${135^ \circ }$.