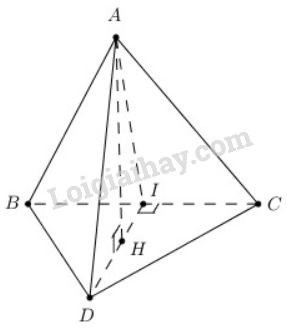
Bài 2 trang 104 SGK Hình học 11

Đề bài

Cho tứ diện $ABCD$ có hai mặt $ABC$ và $BCD$ là hai tam giác cân có chung cạnh đáy $BC$.Gọi $I$ là trung điểm của cạnh $BC$.

a) Chứng minh rằng $BC$ vuông góc với mặt phẳng $(ADI)$.

b) Gọi $AH$ là đường cao của tam giác $ADI$, chứng minh rằng $AH$ vuông góc với mặt phẳng $(BCD)$.

Lời giải chi tiết

a) Tam giác $ABC$ cân tại $A$ nên ta có đường trung tuyến ứng với cạnh đáy đồng thời là đường cao do đó: $AI\bot BC$

Tương tự ta có: $DI\bot BC$

Ta có:

$\left. \matrix{ AI \bot BC \hfill \cr DI \bot BC \hfill \cr AI \cap DI = {\rm{\{ }}I{\rm{\} }} \hfill \cr} \right\} \Rightarrow BC \bot (ADI)$

b) Ta có $AH$ là đường cao của tam giác $ADI$ nên $AH\bot DI$

Mặt khác: $BC\bot (ADI)$ mà $AH\subset (ADI)$ nên $AH\bot BC$

Ta có 

$\left. \matrix{ AH \bot BC \hfill \cr AH \bot DI \hfill \cr BC \cap DI = {\rm{\{ }}I{\rm{\} }} \hfill \cr} \right\} \Rightarrow AH \bot (BCD)$

HocTot.Nam.Name.Vn