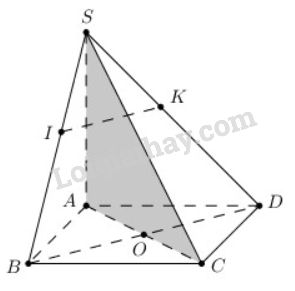
Bài 6 trang 105 SGK Hình học 11

Đề bài

Cho hình chóp $S.ABCD$ có đáy là hình thoi $ABCD$ và có cạnh $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $I$ và $K$ là hai điểm lần lượt lấy trên hai cạnh $SB$ và $SD$ sao cho $\dfrac{SI}{SB}=\dfrac{SK}{SD}.$ Chứng minh:

a) $BD$ vuông góc với $SC$; 

b) $IK$ vuông góc với mặt phẳng $(SAC)$.

Lời giải chi tiết

a) $ABCD$ là hình thoi nên $AC\bot BD$    (1)

Theo giả thiết: $SA\bot (ABCD)\Rightarrow SA\bot BD$        (2)

Từ (1) và (2) suy ra  $BD ⊥ SC$ (Tính chất một đường vuông góc với 2 cạnh của một tam giác thì vuông góc với cả cạnh còn lại của tam giác ấy)

Cách khác:

Sử dụng định lí ba đường vuông góc:

Ta có: $SA \bot \left( {ABCD} \right)$ $\Rightarrow AC$ là hình chiếu của $SC$ lên $(ABCD)$.

Mà $BD \bot AC \Rightarrow BD \bot SC$

b) Ta có: $\dfrac{SI}{SB}=\dfrac{SK}{SD}$ theo định lí Ta-lét ta có $IK//BD$

Theo a) ta có: $BD ⊥ (SAC) \Rightarrow IK ⊥ (SAC)$.

HocTot.Nam.Name.Vn