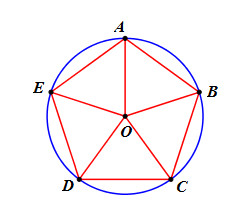
Bài 15 trang 103 Tài liệu dạy – học Toán 9 tập 2Giải bài tập Chứng minh GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Chứng minh \(\widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = \widehat {ODE} = \widehat {ODE} = \widehat {OEA} = \widehat {OAE}\) Từ đó chứng minh nếu một ngũ giác nội tiếp và có các cạnh bằng nhau thì nó có phải là ngũ giác đều. Phương pháp giải - Xem chi tiết Chứng minh ngũ giác ABCDE có tất cả các góc bằng nhau. Lời giải chi tiết Ta có : \(AB = BC = CD = DE = EA \) \(\Rightarrow cung\,AB = cung\,BC = cung\,CD = cung\,DE = cung\,EA\) (các dây bằng nhau căng các cung bằng nhau). \( \Rightarrow \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA}\) (số đo góc ở tâm bằng số đo cung bị chắn). Xét \(\Delta OAB\) có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O. \( \Rightarrow \widehat {OAB} = \widehat {OBA} = \dfrac{{{{180}^0} - \widehat {OAB}}}{2}\). Chứng minh tương tự ta có \(\begin{array}{l}\widehat {OBC} = \widehat {OCB} = \dfrac{{{{180}^0} - \widehat {BOC}}}{2}\\\widehat {OCD} = \widehat {ODC} = \dfrac{{{{180}^0} - \widehat {COD}}}{2}\\\widehat {ODE} = \widehat {ODE} = \dfrac{{{{180}^0} - \widehat {DOE}}}{2}\\\widehat {OEA} = \widehat {OAE} = \dfrac{{{{180}^0} - \widehat {EOA}}}{2}\end{array}\) Mà \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA}\) \(\begin{array}{l} \Rightarrow \widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = \widehat {ODE} = \widehat {ODE} = \widehat {OEA} = \widehat {OAE}\\ \Rightarrow \widehat {EAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA}\end{array}\) Vậy ngũ giác ABCDE là ngũ giác đều (Ngũ giác có tất cả các cạnh bằng nhau và các góc bằng nhau). HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|