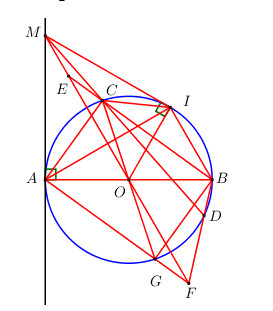
Bài 11 trang 103 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Cho đường tròn (O) đường kính AB. Từ điểm M khác điểm A trên tiếp tuyến với đường tròn tại A, ta vẽ cát tuyến MCD (C nằm giữa M và D). Vẽ tiếp tuyến MI tiếp xúc với (O) tại I. Đường thẳng BC và BD cắt đường thẳng OM tại E và F. Chứng minh:

a) MICE là tứ giác nội tiếp.

b) O là trung điểm của EF.

Lời giải chi tiết

 

a) Ta có $OA = OI = R \Rightarrow O$ thuộc trung trực của AI.

$MA = MI$ (tính chất 2 tiếp tuyến cắt nhau) $\Rightarrow$ M thuộc trung trực của AI.

$\Rightarrow OM$ là trung trực của AI $\Rightarrow OM \bot AI$.

Ta có : $\widehat {AIB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow IB \bot AI$

$\Rightarrow OM//IB \Rightarrow \widehat {IBC} = \widehat {CEO}$ (hai góc so le trong bằng nhau).

Lại có $\widehat {IBC} = \widehat {CIM}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung IC)

$\Rightarrow \widehat {CEO} = \widehat {CIM}$$\left( { = \widehat {IBC}} \right)$.

Mà $\widehat {CEO} + \widehat {CEM} = {180^0}$  (hai góc kề bù) $\Rightarrow \widehat {CIM} + \widehat {CEM} = {180^0} \Rightarrow$Tứ giác MICE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰).

b) Gọi G là giao điểm của AF và đường tròn $\left( O \right)$. Xét tứ giác ACBG nội tiếp đường tròn $\left( O \right)$ có $\widehat {ABC} = \widehat {AGC}$ (hai góc nội tiếp cùng chắn cung AC).

Mà tam giác OAG cân tại O (do $OA = OG$) $\Rightarrow \widehat {AGC} = \widehat {OAG} \Rightarrow \widehat {ABC} = \widehat {OAG}$.

Ta có: $\widehat {ACB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \Delta ABC$ vuông tại C $\Rightarrow \widehat {ABC} + \widehat {BAC} = {90^0}$

$\Rightarrow \widehat {OAG} + \widehat {BAC} = {90^0}$

$\Rightarrow \widehat {CAG} = {90^0}$ $\Rightarrow AG \bot AC$. Mà $AC \bot BC\,\,\left( {\widehat {ACB} = {{90}^0}} \right) \Rightarrow AG//BC$.

Và $\widehat {CAG}$ nội tiếp chắn nửa đường tròn $\Rightarrow O$ là trung điểm của CG $\Rightarrow OC = OG$

Áp dụng định lí Ta-lét ta có: $\dfrac{{OE}}{{OF}} = \dfrac{{OC}}{{OG}} = 1 \Rightarrow OE = OF$. Vậy O là trung điểm của EF.

 HocTot.Nam.Name.Vn