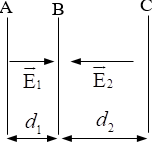
Phương pháp giải bài tập về điện thế - hiệu điện thế

Dạng bài: Tìm điện thế - hiệu điện thế

Sử dụng các công thức sau:

- Điện thế: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)

Điện thế tại một điểm gây bởi điện tích q: \({V_M} = k\frac{q}{{\varepsilon r}}\)

Điện thế do nhiều điện tích gây ra: \(V = {V_1} + {V_2} + ... + {V_M}\)

Lưu ý: Người ta luôn chọn mốc điện thế tại mặt đất và ở vô cùng (bằng 0)

- Hiệu điện thế: \({U_{MN}} = \frac{{{A_{MN}}}}{q} = {V_M} - {V_N}\)

- Công thức liên hệ giữa cường độ điện trường và hiệu điện thế trong điện trường đều: \(E = \frac{U}{d}\)

Lưu ý: Trong điện trường, vecto cường độ điện trường có hướng từ nơi có điện thế cao sang nơi có điện thế thấp.

Bài tập ví dụ:

Cho ba bản kim loại phẳng A,B,C đặt song song như hình vẽ, cho d₁ = 5 cm và d₂ = 8 cm. Các bản được tích điện và điện tường giữa các bản là đều, có chiều như hình vẽ với độ lớn: \({E_1} = {4.10^4}V/m,{E_2} = {5.10^4}V/m\). Chọn gốc điện thế tại bản A, tìm điện thế \({V_B},{V_C}\) của hai bản B,C.

Hướng dẫn giải

Từ hình vẽ ta thấy \(\overrightarrow {{E_1}} \) hướng từ A đến B nên ta có: \({U_{AB}} = {V_A} - {V_B} = {E_1}.{d_1}\)

Chọn gốc điện thế tại A => \({V_A} = 0\)

\( \Rightarrow {V_B} = {V_A} - {E_1}{d_1} = 0 - {4.10^4}{.5.10^{ - 2}} =  - 2000V\)

\(\overrightarrow {{E_2}} \) hướng từ C đến B nên ta có:

\({U_{CB}} = {V_C} - {V_B} = {E_2}{d_2} \Leftrightarrow {V_C} = {V_B} + {E_2}{d_2} \\=  - 2000 + {5.10^4}{.8.10^{ - 2}} = 2000V\)