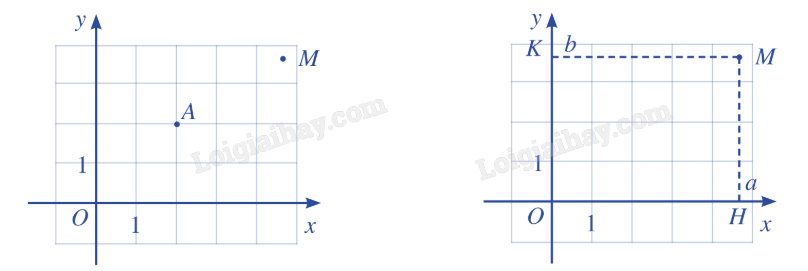
Lý thuyết Tọa độ của vecto - SGK Toán 10 Cánh diềuA. Lý thuyết 1. Tọa độ của một điểm Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... A. Lý thuyết 1. Tọa độ của một điểm
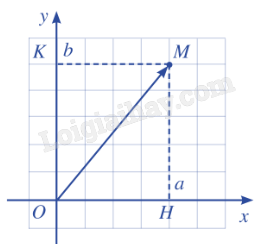
2. Tọa độ của một vecto
→OM=(a;b) thì a là hoành độ, b là tung độ của →OM.
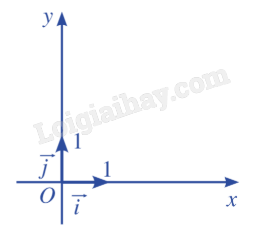
Chú ý: Trong mặt phẳng tọa độ Oxy, ta có: + →OM=(a;b)⇔M(a;b). + Vecto →i(1;0), →j(0;1) có điểm gốc O lần lượt là các vecto đơn vị trên trục Ox, Oy.
Ta có định lí sau:
Chú ý: Với →a=(x1;y1) và →b=(x2;y2), ta có: →a=→b⇔{x1=x2y1=y2. Như vậy, mỗi vecto hoàn toàn được xác định khi biết tọa độ của nó. 3. Liên hệ giữa tọa độ của điểm và tọa độ của vecto
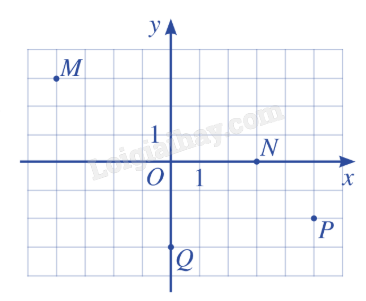
B. Bài tập Bài 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M, N, P, Q. Tìm tọa độ các vecto →OM, →ON, →OP, →OQ.
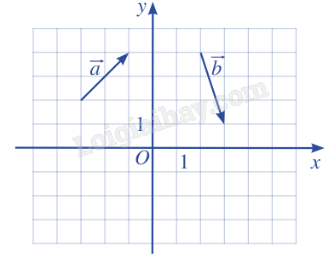
Giải: Từ hình vẽ, ta có: M(-4;3), N(3;0), P(5;-2), Q(0;-3). Do đó: →OM=(−4;3), →ON=(3;0), →OP=(5;−2), →OQ=(0;−3). Bài 2: Tìm tọa độ của các vecto →a, →b trong hình.
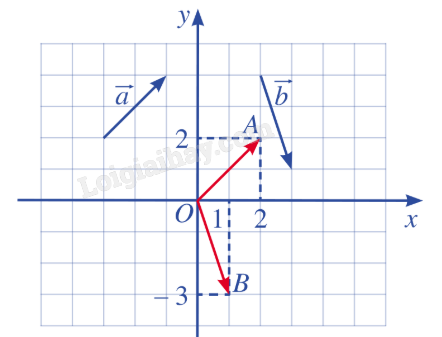
Giải: Ta có: →a=→OA và A(2;2); tọa độ vecto →OA chính là tọa độ điểm A nên →a=(2;2). →b=→OB và A(1;-3); tọa độ vecto →OB chính là tọa độ điểm B nên →b=(1;−3).
Bài 3: Trong mặt phẳng tọa độ Oxy, cho điểm A(1;2) và vecto →u=(3;−4). a) Biểu diễn vecto →u qua hai vecto →i và →j. b) Biểu diễn vecto →OA qua hai vecto →i và →j. Giải: a) Vì →u=(3;−4) nên →u=3→i+(−4)→j=3→i−4→j. b) Vì điểm A có tọa độ là (1;2) nên →OA=(1;2). Do đó: →OA=1→i+2→j=→i+2→j. Bài 4: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(1;1), B(4;3), C(-1;-2). a) Tìm tọa độ của vecto →AB. b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành. Giải: a) Ta có: →AB=(4−1;3−1). Vậy →AB=(3;2). b) Gọi tọa độ của điểm D là (xD;yD), ta có: →DC=(−1−xD;−2−yD). Tứ giác ABCD là hình bình hành khi và chỉ khi: →DC=→AB⇔→DC=(3;2)⇔{−1−xD=3−2−yD=2⇔{xD=−4yD=−4. Vậy D(-4;-4). 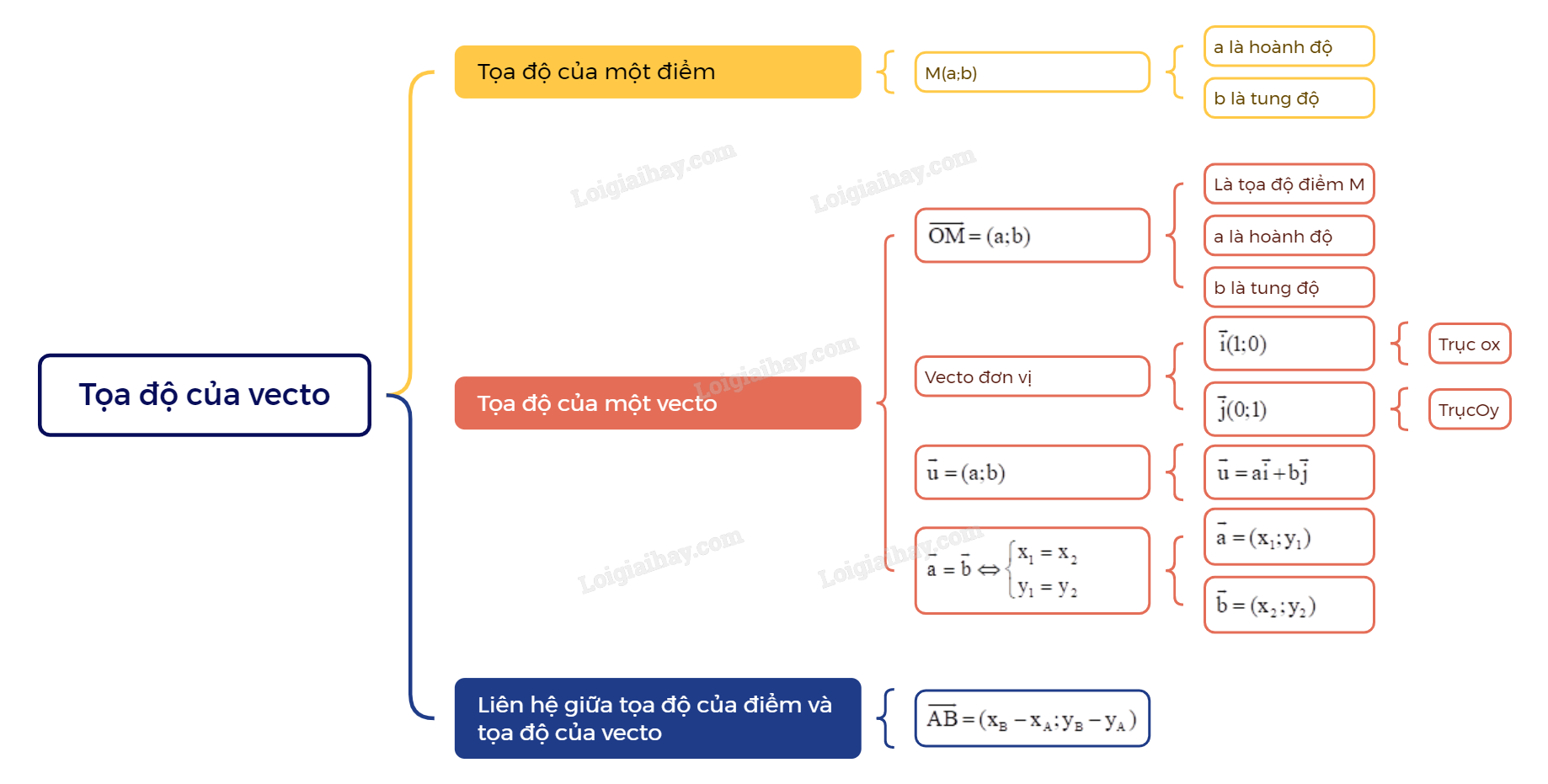
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|