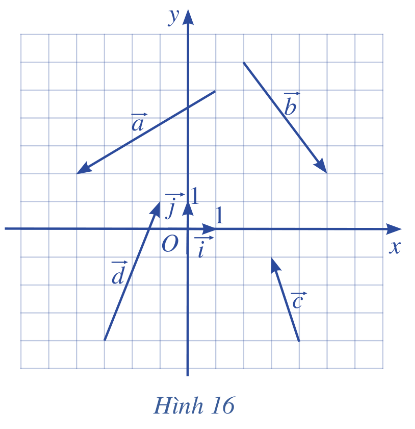
Giải bài 1 trang 65 SGK Toán 10 tập 2 – Cánh diềuTìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto →i,→j
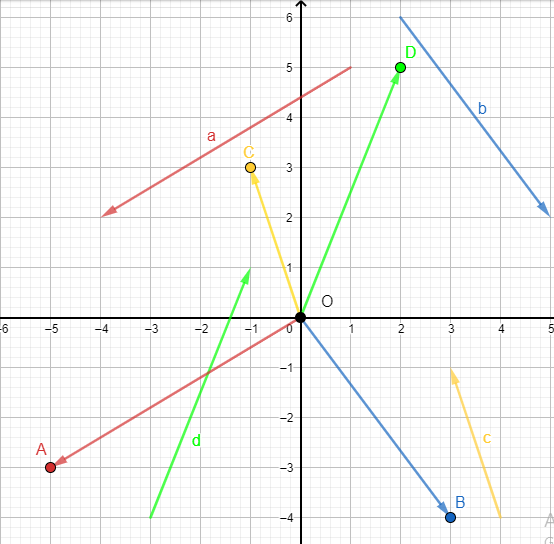
Phương pháp giải - Xem chi tiết Vẽ các vecto →OA=→a,→OB=→b,→OC=→c,→OD=→d. Tọa độ của 4 điểm A, B, C, D là tọa độ của 4 vecto. Để biểu diễn các vecto qua vecto đơn vị: →u=(a;b)⇔→u=a→i+b→j Lời giải chi tiết a) Vẽ các vecto →OA=→a,→OB=→b,→OC=→c,→OD=→d
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm A, B, C, D là: A(−5;−3),B(3;−4),C(−1;3),D(2;5) Do đó →a=→OA=(−5;−3),→b=→OB=(3;−4),→c=→OC=(−1;3),→d=→OD=(2;5) b) Vì →a=→OA=(−5;−3)nên →a=(−5)→i+(−3)→j=−5→i−3→j Vì →b=→OB=(3;−4) nên →b=3→i+(−4)→j=3→i−4→j Vì →c=→OC=(−1;3) nên →c=(−1)→i+(3)→j=−→i+3→j Vì →d=→OD=(2;5) nên →d=2→i+5→j
|