Lý thuyết tính chất đường phân giác của tam giácLý thuyết: Tính chất đường phân giác của tam giác 1. Các kiến thức cần nhớ  Định lý: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy. Chú ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác. Ví dụ: Cho tam giác \(ABC\) có \(AD,\,AE\) lần lượt là đường phân giác góc trong và góc ngoài tại đỉnh \(A\) . Khi đó ta có $\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}$ và $\dfrac{{EB}}{{EC}} = \dfrac{{AB}}{{AC}}$ 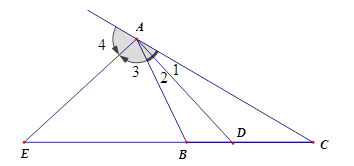 2. Các dạng toán thường gặp Dạng 1: Tính độ dài cạnh, chu vi, diện tích Phương pháp: Sử dụng tính chất đường phân giác của tam giác và tỉ lệ thức để biến đổi và tính toán. + Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy. Dạng 2: Chứng minh đẳng thức hình học và các bài toán khác Phương pháp: Sử dụng tính chất đường phân giác của tam giác: “Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.”
 Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
