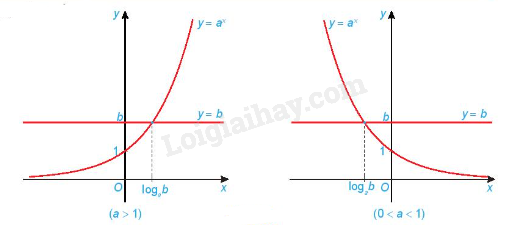
Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Kết nối tri thức1. Phương trình mũ Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh 1. Phương trình mũ Phương trình mũ cơ bản có dạng ax=b(với 0<a≠1). - Nếu b > 0 thì phương trình có nghiệm duy nhất x=logab. - Nếu b ≤ 0 thì phương trình vô nghiệm. Minh họa bằng đồ thị:
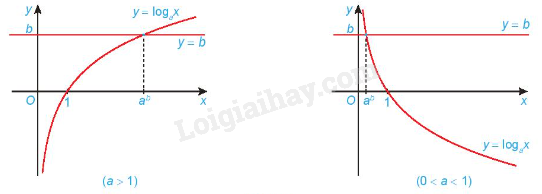
Chú ý: Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số: Nếu 0<a≠1 thì au=av⇔u=v. 2. Phương trình lôgarit Phương trình lôgarit cơ bản có dạng logax=b(0<a≠1). Phương trình lôgarit cơ bản logax=b có nghiệm duy nhất x=ab. Minh họa bằng đồ thị:
Chú ý: Phương pháp giải phương trình lôgarit bằng cách đưa về cùng cơ số: Nếu u,v>0 và 0<a≠1 thì logau=logav⇔u=v. 3. Bất phương trình mũ Bất phương trình mũ cơ bản có dạng ax>b (hoặc ax≥b,ax<b,ax≤b) với a>0,a≠1. Xét bất phương trình dạng ax>b: - Nếu b≤0 thì tập nghiệm của bất phương trình là R. - Nếu b > 0 thì bất phương trình tương đương với ax>alogab. Với a > 1, nghiệm của bất phương trình là x>logab. Với 0<a<1, nghiệm của bất phương trình là x<logab. Chú ý: a) Các bất phương trình mũ cơ bản còn lại được giải tương tự. b) Nếu a > 1 thì au>av⇔u>v. Nếu 0 < a < 1 thì au>av⇔u<v. 4. Bất phương trình lôgarit Bất phương trình lôgarit cơ bản có dạng logax>b(hoặc logax≥b,logax<b,logax≤b) với a>0,a≠1. Xét bất phương trình dạng logax>b: - Nếu a > 1 thì nghiệm của bất phương trình là x>ab. - Nếu 0 < a < 1 thì nghiệm của bất phương trình là 0<x<ab. Chú ý: a) Các bất phương trình lôgarit cơ bản còn lại được giải tương tự. b) Nếu a > 1 thì logau>logav⇔u>v>0. Nếu 0 < a < 1 thì logau>logav⇔0<u<v. 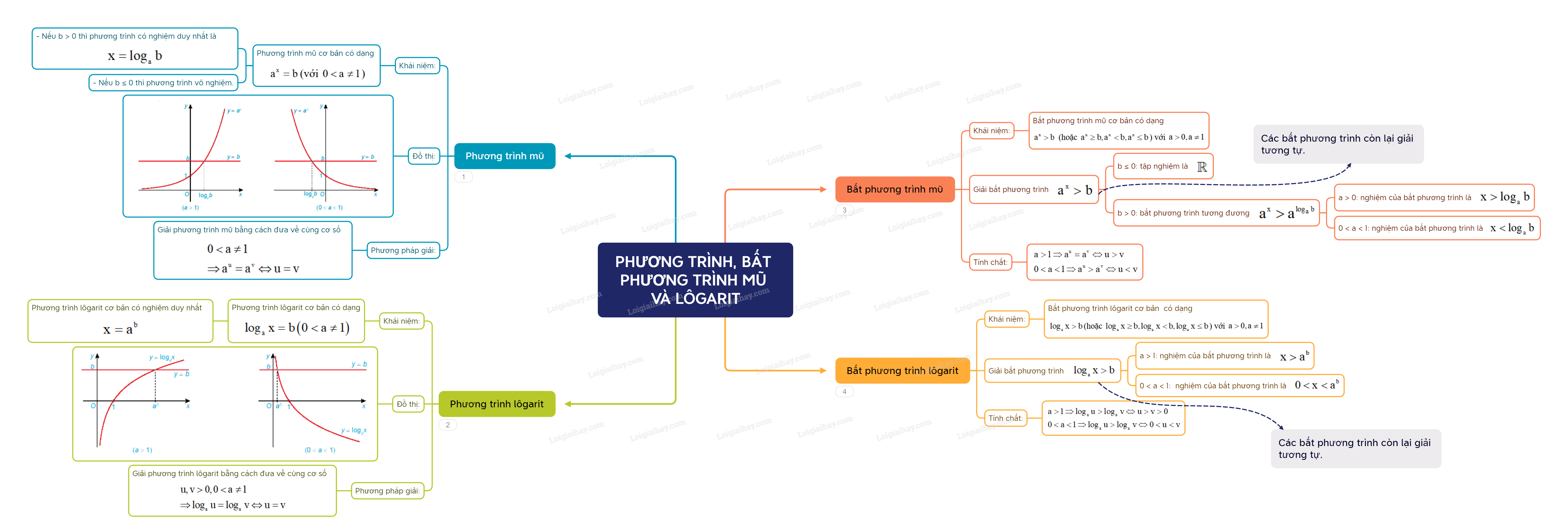
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|