Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Cánh diều1. Phương trình mũ Phương trình mũ cơ bản ẩn x có dạng \({a^x} = b\left( {a > 0,a \ne 1} \right)\). Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh 1. Phương trình mũ Phương trình mũ cơ bản ẩn x có dạng \({a^x} = b\left( {a > 0,a \ne 1} \right)\). - Nếu \(b \le 0\) thì phương trình vô nghiệm. - Nếu \(b > 0\) thì phương trình có nghiệm duy nhất \(x = {\log _a}b\). Với \(a > 0,a \ne 1\) thì
2. Phương trình lôgarit Phương trình lôgarit cơ bản ẩn x có dạng \({\log _a}x = b\left( {a > 0,a \ne 1} \right)\). Phương trình có nghiệm duy nhất \(x = {a^b}\). Với \(a > 0,a \ne 1\) thì
3. Bất phương trình mũ Xét bất phương trình mũ \({a^x} > b\left( {a > 0,a \ne 1} \right)\). - Nếu \(b \le 0\), tập nghiệm của bất phương trình là \(\mathbb{R}\); - Nếu b > 0, a > 1 thì nghiệm của bất phương trình là \(x > {\log _a}b\); - Nếu b > 0, 0 < a < 1 thì nghiệm của bất phương trình là \(x < {\log _a}b\). Các bất phương trình mũ cơ bản khác được giải tương tự. 4. Bất phương trình lôgarit Xét bất phương trình lôgarit \({\log _a}x > b\left( {a > 0,a \ne 1} \right)\). - Nếu a > 1 thì nghiệm của bất phương trình là \(x > {a^b}\). - Nếu 0 < a < 1 thì nghiệm của bất phương trình là 0 < x < \({a^b}\). Các bất phương trình lôgarit cơ bản khác được giải tương tự. 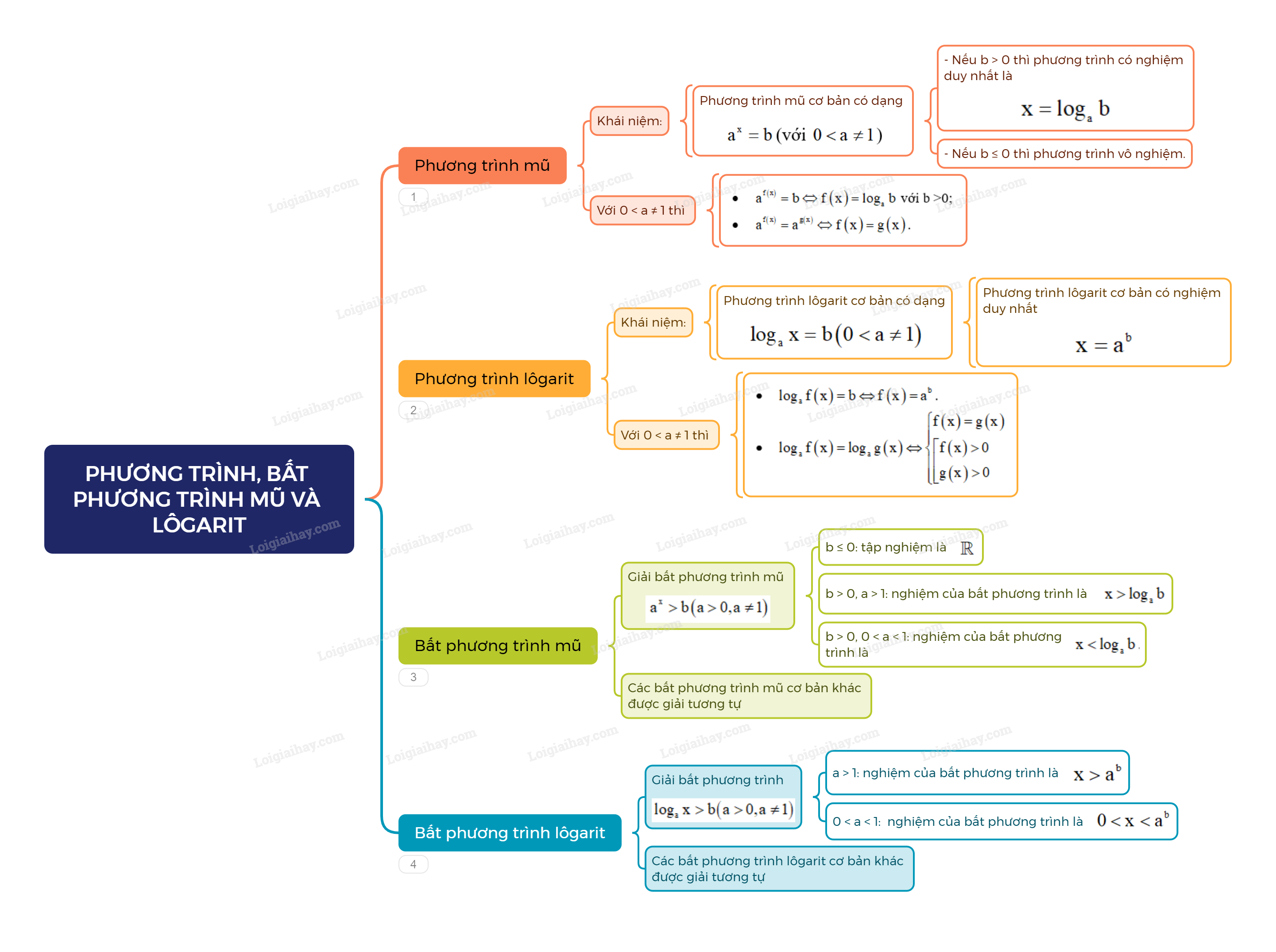
|













