Lý thuyết phép trừ các phân thức đại số1. Phân thức đối. 1. Phân thức đối Hai phân thức được gọi là đối nhau nếu tổng của chúng bằng \(0\). Phân thức đối của phân thức \( \dfrac{A}{B}\) được kí hiệu là \( -\dfrac{A}{B}\) Vậy \( -\dfrac{A}{B} =\dfrac{-A}{B}\) và \( -\dfrac{-A}{B}=\dfrac{A}{B}\) Ví dụ: \(\dfrac{x}{x-2}\) là phân thức đối của phân thức \(\dfrac{-x}{x-2}\) 2. Phép trừ Quy tắc: Muốn trừ phân thức \( \dfrac{A}{B}\) cho phân thức \( \dfrac{C}{D}\), ta cộng \( \dfrac{A}{B}\) với phân thức đối của \( \dfrac{C}{D}\) Vậy: \( \dfrac{A}{B}-\dfrac{C}{D}=\dfrac{A}{B}+\left( { - \dfrac{C}{D}} \right)\). Ví dụ: \( \dfrac{4x-1}{3x^{2}y}-\dfrac{7x-1}{3x^{2}y}\) \( =\dfrac{4x-1}{3x^{2}y}+\dfrac{-(7x-1)}{3x^{2}y}\) \( =\dfrac{4x-1-7x+1}{3x^{2}y}\) \( =\dfrac{-3x}{3x^{2}y}=-\dfrac{1}{xy}\).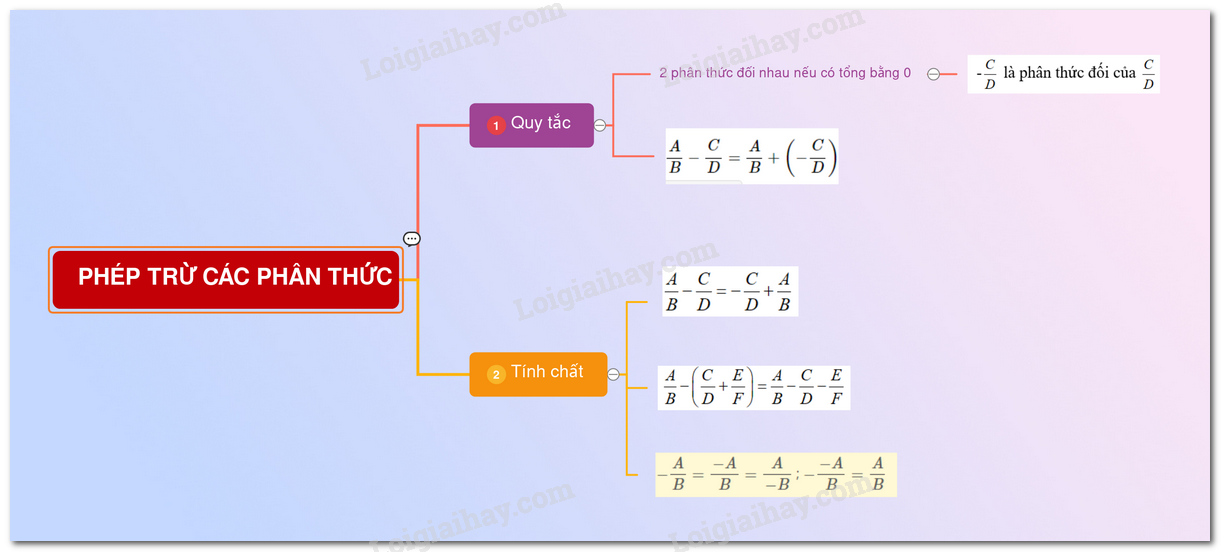
 Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
