Lý thuyết phép chia các phân thức đại số

1. Các kiến thức cần nhớ 

a) Nhân hai phân thức

Ví dụ:

$\dfrac{{x - 1}}{x}.\dfrac{3}{{x + 1}}$$= \dfrac{{3\left( {x - 1} \right)}}{{x\left( {x + 1} \right)}}$$= \dfrac{{3x - 3}}{{x\left( {x + 1} \right)}}$

b) Chia hai phân thức

* Phân thức nghịch đảo

+ Hai phân thức gọi là nghịch đảo của nhau nếu tích của nó bằng $1$ .

+ Phân thức nghịch đảo của phân thức $\dfrac{A}{B}$ là $\dfrac{B}{A}$ với $A,\,B \ne 0$.

* Phép chia hai phân thức

Ví dụ: $\dfrac{{x - 1}}{x}:\dfrac{3}{{x + 1}} = \dfrac{{x - 1}}{x}.\dfrac{{x + 1}}{3} = \dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x.3}} = \dfrac{{{x^2} - 1}}{{3x}}$

2. Các dạng toán thường gặp

Dạng 1: Thực hiện phép tính. Rút gọn biểu thức

Phương pháp:

Bước 1: Phân tích đa thức thành nhân tử (nếu cần)

Bước 2: Sử dụng quy tắc nhân và chia các phân thức.

+ $\dfrac{A}{B}.\dfrac{C}{D} = \dfrac{{A.C}}{{B.D}}$

+ $\dfrac{A}{B}:\dfrac{C}{D} = \dfrac{A}{B}.\dfrac{D}{C};\,\,\left( {\dfrac{C}{D} \ne 0} \right)$

Dạng 2: Tính giá trị biểu thức tại giá trị cho trước của biến

Phương pháp:

Bước 1: Rút gọn biểu thức (sử dụng quy tắc nhân, chia phân thức và phân tích đa thức thành nhân tử)

Bước 2: Thay giá trị của biến vào đa thức đã rút gọn và thực hiện phép tính.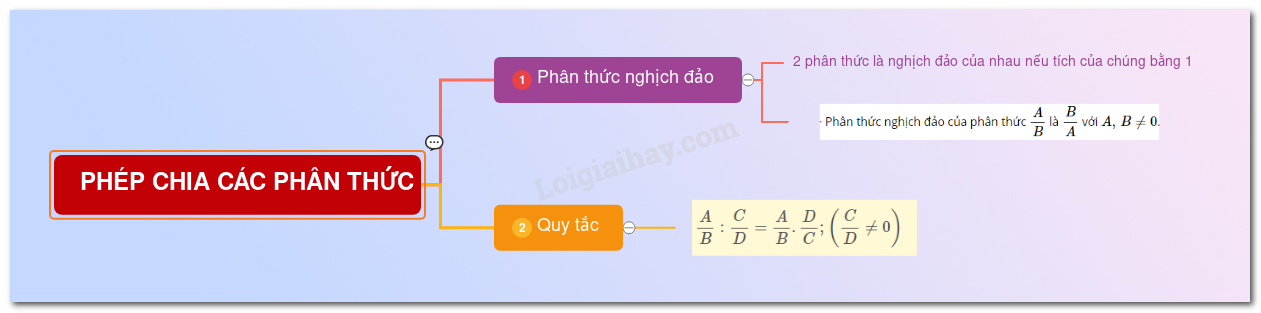