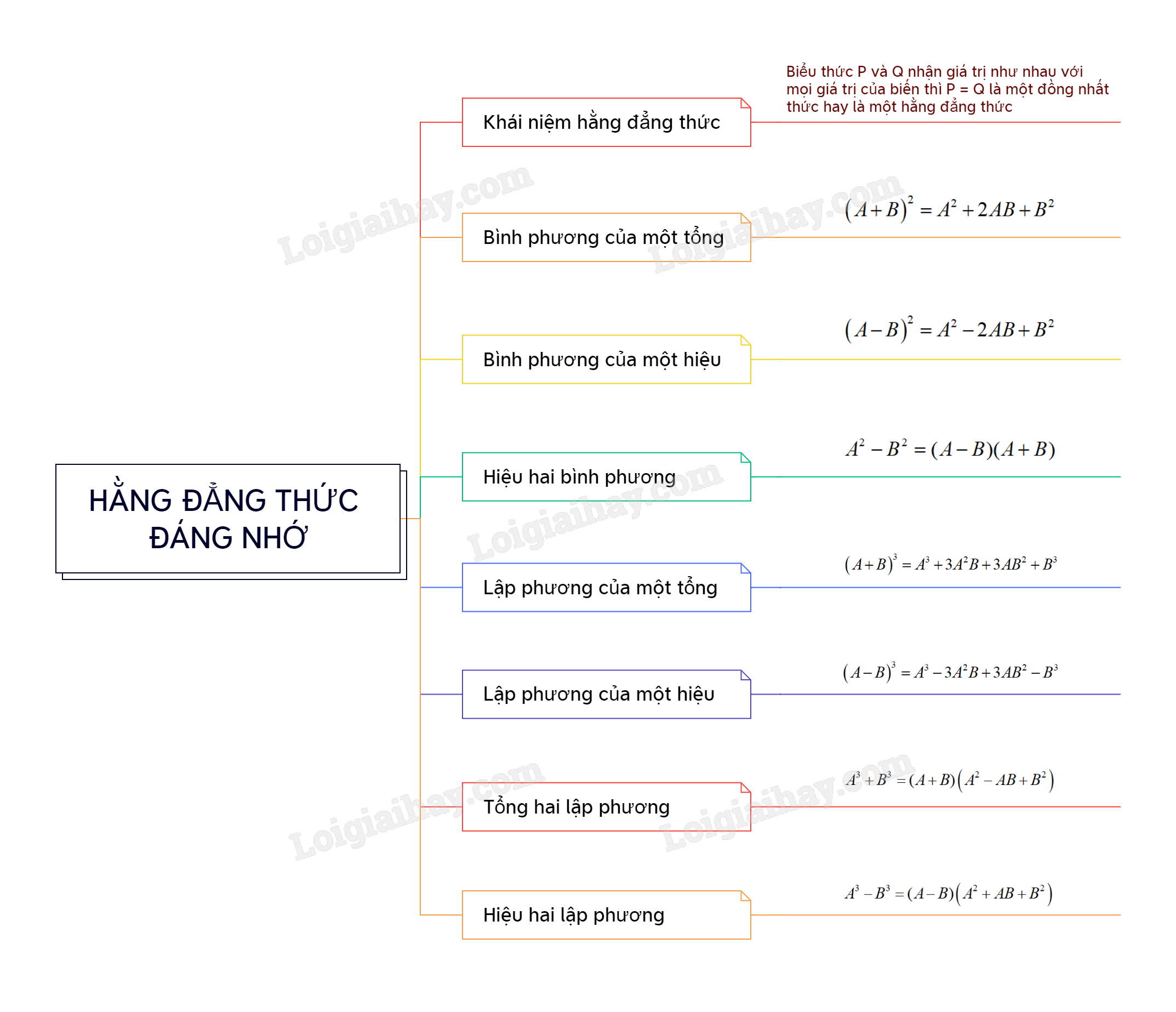
Lý thuyết Những hằng đẳng thức đáng nhớ SGK Toán 8 - Cùng khám phá

1. Hằng đẳng thức

Cho hai biểu thức đại số A và B có cùng các biến. Nếu giá trị của A và giá trị của B luôn bằng nhau tại mọi giá trị của các biến thì ta có một hằng đẳng thức A = B(hay đồng nhất thức)

Ví dụ: \(a + b = b + a;a(a + 2) = {a^2} + 2a\) là những hằng đẳng thức.

\({a^2} - 1 = 3a;a(a - 1) = 2a\) không phải là những hằng đẳng thức.

2. Những hằng đẳng thức đáng nhớ

+ Bình phương của một tổng 

\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

Ví dụ: \({101^2} = {(100 + 1)^2} = {100^2} + 2.100.1 + {1^2} = 10201\)

+ Bình phương của một hiệu 

\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

Ví dụ: \({99^2} = {(100 - 1)^2} = {100^2} - 2.100.1 + {1^2} = 9801\)

+ Hiệu hai bình phương  

\({A^2} - {B^2} = (A - B)(A + B)\)

Ví dụ: \({101^2} - {99^2} = (101 - 99)(101 + 99) = 2.200 = 400\)

+ Lập phương của một tổng  

\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)

Ví dụ: \({\left( {x + 3} \right)^3} = {x^3} + 3{x^2}.3 + 3x{.3^2} + {3^3} = {x^3} + 9{x^2} + 27x + 27\)

+ Lập phương của một hiệu 

\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)

Ví dụ: \({\left( {x - 3} \right)^3} = {x^3} - 3{x^2}.3 + 3x{.3^2} - {3^3} = {x^3} - 9{x^2} + 27x - 27\)

+ Tổng hai lập phương 

\({A^3} + {B^3} = (A + B)\left( {{A^2} - AB + {B^2}} \right)\)

Ví dụ: \({x^3} + 8 = {x^3} + {2^3} = (x + 2)({x^2} - 2x + 4)\)

+ Hiệu hai lập phương 

\({A^3} - {B^3} = (A - B)\left( {{A^2} + AB + {B^2}} \right)\)

Ví dụ: \({x^3} - 8 = \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)\)