Giải mục 2 trang 19, 20, 21, 22, 23, 24 SGK Toán 8 - Cùng khám pháCho
Lựa chọn câu để xem lời giải nhanh hơn
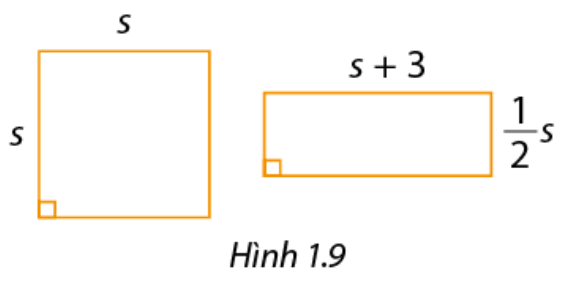
Hoạt động 2 Cho \(a\) và \(b\) là hai số thực bất kì. 1. Thực hiện phép tính \(\left( {a + b} \right)\left( {a + b} \right)\) 2. Hãy cho biết: \({\left( {a + b} \right)^2} = ?\) Phương pháp giải: 1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia. 2. Dựa vào kết quả từ ý 1. Lời giải chi tiết: 1. Ta có \(\left( {a + b} \right)\left( {a + b} \right) = aa + ab + ab + bb = {a^2} + 2ab + {b^2}\) 2. Có \({\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {a + b} \right) = {a^2} + 2ab + {b^2}\) Luyện tập 2 Tính: a) \({\left( {a + 4} \right)^2}\); b) \({\left( {2u + 5v} \right)^2}\) Phương pháp giải: Dựa vào hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) Để thực hiện phép tính. Lời giải chi tiết: a) \({\left( {a + 4} \right)^2} = {a^2} + 2.a.4 + {4^2} = {a^2} + 8a + 16\) b) \({\left( {2u + 5v} \right)^2} = {\left( {2u} \right)^2} + 2.2u.5v + {\left( {5v} \right)^2} = 4{u^2} + 20uv + 25{v^2}\) Luyện tập 3 Viết các biểu thức sau dưới dạng bình phương của một tổng: a) \(16{a^2} + 8a + 1\); b) \({x^2} + 25{y^2} + 10xy\) Phương pháp giải: Dựa vào hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) Để phân tích biểu thức và viết lại dưới dạng bình phương của một tổng. Lời giải chi tiết: a) Ta có \(16{a^2} + 8a + 1 = {\left( {4a} \right)^2} + 2.4a.1 + {1^2} = {\left( {4a + 1} \right)^2}\) b) Ta có\({x^2} + 25{y^2} + 10xy = {x^2} + 2.x.5y + {\left( {5y} \right)^2} = {\left( {x + 5y} \right)^2}\). Hoạt động 3 Cho \(a\) và \(b\) là hai số thực bất kì. 1. Thực hiện phép tính \(\left( {a - b} \right)\left( {a - b} \right)\). 2. Hãy cho biết \({\left( {a - b} \right)^2}\) Phương pháp giải: 1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia. 2. Dựa vào kết quả từ ý 1. Lời giải chi tiết: 1.Ta có \(\left( {a - b} \right)\left( {a - b} \right) = a\left( {a - b} \right) - b\left( {a - b} \right) = {a^2} - ab - ab + {b^2} = {a^2} - 2ab + {b^2}\) 2. Có \({\left( {a - b} \right)^2} = \left( {a - b} \right)\left( {a - b} \right) = {a^2} - 2ab + {b^2}\) Luyện tập 4 Tính: a) \({\left( {3a - 1} \right)^2}\) b) \({\left( {4u - 5v} \right)^2}\) Phương pháp giải: Dựa vào hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Để thực hiện phép tính Lời giải chi tiết: a) \({\left( {3a - 1} \right)^2} = {\left( {3a} \right)^2} - 2.3a.1 + {1^2} = 9{a^2} - 6a + 1\) b) \({\left( {4u - 5v} \right)^2} = {\left( {4u} \right)^2} - 2.4u.5v + {\left( {5v} \right)^2} = 16{u^2} - 40uv + 25{v^2}\) Luyện tập 5 Viết các biểu thức sau dưới dạng bình phương của một hiệu: a) \({a^2} - 12a + 36\); b) \(25{x^2} + 64{y^2} - 80xy\) Phương pháp giải: Dựa vào hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Để viết lại biểu thức dưới dạng bình phương của một hiệu. Lời giải chi tiết: a) Ta có \({a^2} - 12a + 36 = {a^2} - 2.a.6 + {6^2} = {\left( {a - 6} \right)^2}\); b) Ta có \(25{x^2} + 64{y^2} - 80xy = {\left( {5x} \right)^2} - 2.5x.8y + {\left( {8y} \right)^2} = {\left( {5x - 8y} \right)^2}\). Vận dụng 1 Trong Hình 1.9, diện tích của hình vuông là \(9m - 42m + 49\), với \(m > 3\).
a) Tìm độ dài cạnh hình vuông theo \(m\). Từ đó biểu diễn \(s\)theo \(m\). b) Tính diện tích hình chữ nhật trong hình 1.9 theo \(m\). Phương pháp giải: a) Viết lại biểu thức biểu diễn diện tích hình vuông dưới dạng bình phương của một hiệu. Từ đó suy ra độ dài cạnh của hình vuông đó b) Viết biểu thức tính diện tích hình chữ nhật theo công thức tính diện tích hình chữ nhật. Lời giải chi tiết: a) Với \(m > 3\)ta có \(9{m^2} - 42m + 49 = {\left( {3m} \right)^2} - 2.3m.7 + {7^2} = {\left( {3m - 7} \right)^2}\) Vậy độ dài cạnh hình vuông là \(3m - 7\) Vậy \(s = 3m - 7\)
b) Diện tích hình chữ nhật trong hình 1.9 là: \(\left( {s + 3} \right).\frac{1}{2}s = \left( {3m - 7 + 3} \right).\frac{1}{2}\left( {3m - 7} \right) = \frac{1}{2}\left( {3m - 4} \right)\left( {3m - 7} \right)\) \( = \frac{1}{2}\left( {9{m^2} - 21m - 12m + 28} \right) = \frac{1}{2}\left( {9{m^2} - 33m + 28} \right) = \frac{9}{2}{m^2} - \frac{{33}}{2}m + 14\) Vậy diện tích hình chữ nhật trong hình 1.9 là \(\frac{9}{2}{m^2} - \frac{{33}}{2}m + 14\). Hoạt động 4 Cho \(a\) và \(b\) là hai số thực bất kì. 1. \(\left( {a + b} \right)\left( {a - b} \right)\). 2. Hãy cho biết: \({a^2} - {b^2} = ?\) Phương pháp giải: 1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia. 2. Dựa vào kết quả từ ý 1. Lời giải chi tiết: 1. Ta có \(\left( {a + b} \right)\left( {a - b} \right) = a\left( {a - b} \right) + b\left( {a - b} \right) = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\) 2. Vậy \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\) Luyện tập 6 Tính: a) \(\left( {2a + 1} \right)\left( {2a - 1} \right)\) b)\(\left( {2x + 5y} \right)\left( {2x - 5y} \right)\) Phương pháp giải: Sử dụng hằng đẳng thức \(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}\) để thực hiện phép tính. Lời giải chi tiết: a) \(\left( {2a + 1} \right)\left( {2a - 1} \right) = {\left( {2a} \right)^2} - {1^2} = 4{a^2} - 1\) b) \(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = {\left( {2x} \right)^2} - {\left( {5y} \right)^2} = 4{x^2} - 25{y^2}\) Luyện tập 7 Tính nhanh: a) \(49.51\) b) \({32^2} - 128 + 4\) Phương pháp giải: Sử dụng hằng đẳng thức \(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}\) để thực hiện phép tính một cách nhanh nhất Lời giải chi tiết: a) Ta thấy \(49.51 = \left( {50 - 1} \right)\left( {50 + 1} \right) = {50^2} - {1^2} = 2500 - 1 = 2499\) b) \({32^2} - 128 + 4 = {32^2} - 144 = {32^2} - {12^2} = \left( {32 - 12} \right)\left( {32 + 12} \right) = 20.44 = 880\) Vận dụng 2
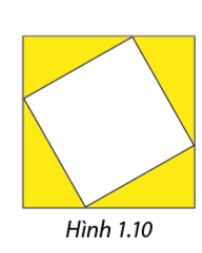
Một người dùng các thanh kim loại để thiết kế một khung ảnh gồm hai hình vuông lồng vào nhau như Hình 1.10, trong đó ảnh được gắn vào hình vuông nhỏ. Biết rằng tổng chiều dài của các thanh kim loại để làm khung là \(168\,\,cm\) và diện tích phần không gắn ảnh( phần tô màu) là \(252\,\,c{m^2}\). Tính diện tích của phần được gắn ảnh. Phương pháp giải:
Gọi độ dài hai cạnh hình vuông lần lượt là\(a\) và \(b\)như hình vẽ Viết biểu thức biểu diễn tổng chiều dài của các thanh kim loại. Viết biểu thức biểu diễn diện tích phần không gắn ảnh. Áp dụng các kiến thức đã học để tính diện tích phần tô màu. Lời giải chi tiết: Gọi độ dài hai cạnh hình vuông lần lượt là \(a\) và \(b\)như hình vẽ \(\left( {cm,a > b > 0} \right)\) Theo đề bài tổng độ dài của các thanh kim loại là \(168cm\)nên ta có: \(4a + 4b = 168 \Rightarrow a + b = 42\)(1) Diện tích phần không gắn ảnh là hiệu diện tích của hình vuông lớn và hình vuông nhỏ và bằng \(252c{m^2}\)nên ta có: \({a^2} - {b^2} = 252 \Rightarrow \left( {a + b} \right)\left( {a - b} \right) = 252 \Rightarrow 42.\left( {a - b} \right) = 252 \Rightarrow a - b = 6\) \( \Rightarrow a = 6 + b\)Thay vào (1) ta có: \(6 + b + b = 42 \Rightarrow 2b = 36 \Rightarrow b = 18 \Rightarrow a = 24\) Diện tích phần không gắn ảnh là: \(4.\frac{1}{2}ab = 2ab\)\(c{m^2}\) Có \(2ab = 252\) nên \(ab = 126 \Rightarrow a = \frac{{126}}{b}\) Thay \(a = \frac{{126}}{b}\)vào (1) ta được \(\begin{array}{l}4.\frac{{126}}{b} + 4b + {\left( {\frac{{126}}{b}} \right)^2} - {b^2} = 168\\ \Rightarrow 504 + 4{b^2} + {126^2} - {b^3}\end{array}\) Diện tích của phần được gắn ảnh là: Hoạt động 5 Cho \(a\) và \(b\)là hai số thực bất kì:
Phương pháp giải: 1. Sử dụng hằng đẳng thức bình phương của một tổng kết hợp với nhân đa thức với đa thức để thực hiện phép tính. 2. Dựa vào kết quả của ý 1. Lời giải chi tiết: 1. \(\left( {a + b} \right){\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {{a^2} + 2ab + {b^2}} \right) = {a^3} + {a^2}b + 2{a^2}b + 2a{b^2} + a{b^2} + {b^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) 2. Có \({\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) Luyện tập 8 Tính: a)\({\left( {2a + 3} \right)^3}\) b)\({\left( {u + 4v} \right)^3}\) Phương pháp giải: Sử dụng hằng đẳng thức \({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) thực hiện phép tính. Lời giải chi tiết: a) \({\left( {2a + 3} \right)^3} = {\left( {2a} \right)^3} + 3.{\left( {2a} \right)^2}.3 + 3.2a{.3^2} + {3^3} = 8{a^3} + 36{a^2} + 54a + 27\) b) \({\left( {u + 4v} \right)^3} = {u^3} + 3.{u^2}.4v + 3.u.{\left( {4v} \right)^2} + {\left( {4v} \right)^3} = {u^3} + 12{u^2}v + 48u{v^2} + 64{v^3}\) Hoạt động 6 Cho \(a\) và \(b\) là hai số thực bất kì. 1. Thực hiện phép tính \({\left[ {a + \left( { - b} \right)} \right]^3}\). 2. Hãy cho biết: \({\left( {a - b} \right)^3} = ?\). Phương pháp giải: 1. Ta nhân đa thức với đa thức kết hợp với sử dụng hằng đẳng thức bình phương của một hiệu: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia. 2. Dựa vào kết quả từ ý 1. Lời giải chi tiết: 1.Ta có: \(\begin{array}{l}{\left[ {a + \left( { - b} \right)} \right]^3} = {\left( {a - b} \right)^2}\left( {a - b} \right) = \left( {{a^2} - 2ab + {b^2}} \right)\left( {a - b} \right)\\ = {a^3} - 2{a^2}b + a{b^2} + 2a{b^2} - {a^2}b - {b^3}\\ = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\) 2. \({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}.\) Luyện tập 9 Tính: a) \({\left( {a - 3} \right)^3};\) b) \({\left( {3u - 4v} \right)^3}.\) Phương pháp giải: Sử dụng hằng đẳng thức \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) thực hiện phép tính. Lời giải chi tiết: a) \(\begin{array}{l}{\left( {a - 3} \right)^3} = {a^3} - 3.{a^2}.3 + 3.a{.3^2} - {3^3}\\ = {a^3} - 9{a^2} + 27a - 27\end{array}\) b) \(\begin{array}{l}{\left( {3u - 4v} \right)^3} = {\left( {3u} \right)^3} - 3.{\left( {3u} \right)^2}.4v + 3.3u.{\left( {4v} \right)^2} - {\left( {4v} \right)^2}\\ = 27{u^3} - 108{u^2}v + 144u{v^2} - 64{v^3}\end{array}\) Hoạt động 7 Cho \(a\) và \(b\) là hai số thực bất kì. 1. Thực hiện phép tính \(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right).\) 2. Hãy cho biết \({a^3} + {b^3} = ?\) Phương pháp giải: 1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia. 2. Dựa vào kết quả từ ý 1. Lời giải chi tiết: 1. Ta có: \(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) = {a^3} - {a^2}b + a{b^2} + {a^2}b - a{b^2} + {b^3} = {a^3} + {b^3}.\) 2. \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\) Luyện tập 10 a) Viết \(8{a^3} + 27\) dưới dạng tích. b) Viết \(\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)\) dưới dạng tổng. Phương pháp giải: Sử dụng hằng đẳng thức \({A^3} + {B^3} = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)\) thực hiện phép tính. Lời giải chi tiết: a) \(8{a^3} + 27 = {\left( {2a} \right)^3} + {3^3} = \left( {2a + 3} \right)\left( {4{a^2} - 6a + 9} \right)\) b) \(\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right) = {x^3} + 27\) Hoạt động 8 Cho \(a\) và \(b\) là hai số thực bất kì. a) Thực hiện phép tính \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\) b) \({a^3} - {b^3} = ?\) Phương pháp giải: 1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia. 2. Dựa vào kết quả từ ý 1. Lời giải chi tiết: 1. \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) = {a^3} + {a^2}b + a{b^2} - {a^2}b - a{b^2} - {b^3} = {a^3} - {b^3}.\) 2. \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\) Luyện tập 11 a) Tính \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right).\) b) Viết \(64{x^3} - 27{y^3}\) dưới dạng tích. Phương pháp giải: Sử dụng hằng đẳng thức \({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\) thực hiện phép tính. Lời giải chi tiết: a) \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right) = {a^3} - {4^3} = {a^3} - 64\) b) \(64{x^3} - 27{y^3} = {\left( {4x} \right)^3} - {\left( {3y} \right)^3} = \left( {4x - 3y} \right)\left( {16{x^2} - 12xy + 9{y^2}} \right)\)
|