Lý thuyết Nhị thức Newton - SGK Toán 10 Chân trời sáng tạo

A. Lý thuyết

1. Một số công thức khai triển

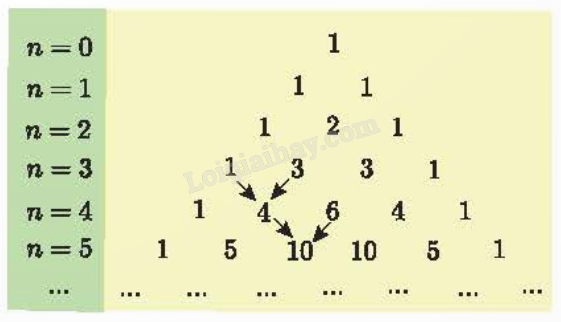
Những công thức khai triển nói trên là công thức nhị thức Newton ${(a + b)^n}$ ứng với n = 4 và n = 5.

Chú ý: Các hệ số trong khai triển nhị thức Newton ${(a + b)^n}$ với n = 0; 1; 2; 3;… được viết thành từng hàng và xếp thành bảng số dưới đây. Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của hai số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũ tên trên bảng). Bảng số này được gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lý học, triết học người Pháp Blaise Pascal, 1623 – 1662).

2. Công thức khai triển tổng quát

Nhận xét:

- Số hạng tổng quát trong khai triển của ${(a + b)^n}$ đều có dạng $C_n^k{a^{n - k}}{b^k}$ $(0 \le k \le n)$.

- Từ công thức nhị thức Newton nói trên, ta có khai triển của ${(a - b)^n}$ như sau:

${(a - b)^n} = C_n^0{a^n} - C_n^1{a^{n - 1}}b + C_n^2{a^{n - 2}}{b^2} - C_n^3{a^{n - 3}}{b^3} + ...$, ở đó các dấu “+”, “-“ xen kẽ nhau.

Ví dụ: ${(a - b)^3} = C_3^0{a^3} - C_3^1{a^{3 - 1}}b + C_3^2{a^{3 - 2}}{b^2} - C_3^3{a^{3 - 3}}{b^3} = C_3^0{a^3} - C_3^1{a^2}b + C_3^2a{b^2} - C_3^3{b^3}$.

Có thể xem thêm trong chuyên đề học tập Toán 10.

B. Bài tập

Bài 1: Khai triển biểu thức ${(x + 1)^4}$.

Giải:

Xác định số hạng: a = x, b = 1.

${(x + 1)^4} = C_4^0{x^4} + C_4^1{x^3}.1 + C_4^2{x^2}{.1^2} + C_4^3{x^1}{.1^3} + C_4^4{.1^4} = {a^4} + 4{x^3} + 6{x^2} + 4x + 1$.

Bài 2: Khai triển biểu thức ${(x - 1)^4}$.

Giải:

Có hai cách khai triển, tùy thuộc vào việc đặt b = -1 hay b = 1.

Nếu coi a = x, b = -1:

${(x - 1)^4} = C_4^0{x^4} + C_4^1{x^3}.( - 1) + C_4^2{x^2}.{( - 1)^2} + C_4^3{x^1}.{( - 1)^3} + C_4^4.{( - 1)^4} = {a^4} - 4{x^3} + 6{x^2} - 4x + 1$.

Hoặc có thể coi a = x, b = 1 và áp dụng công thức khai triển tổng quát:

$${(a - b)^n} = C_n^0{a^n} - C_n^1{a^{n - 1}}b + C_n^2{a^{n - 2}}{b^2} - C_n^3{a^{n - 3}}{b^3} + ...$$ , khi đó sẽ nhận được kết quả như trên (xen kẽ dấu).

Bài 3:

a) Khai triển biểu thức ${(x - 2y)^4}$ và tìm hệ số của số hạng chứa ${y^4}$.

b) Khai triển biểu thức ${(3x - y)^5}$.

Giải:

a) Coi a = x, b = -2y.

${(x - 2y)^4} = {\left[ {x + ( - 2y)} \right]^4} = {x^4} + 4{x^3}( - 2y) + 6{x^2}{( - 2y)^2} + 4x{( - 2y)^3} + {( - 2y)^4}$

$= {x^4} - 8{x^3}y + 24{x^2}{y^2} - 32x{y^3} + 16{y^4}$.

Số hạng chứa ${y^4}$ là $16{y^4}$, hệ số là 16.

b) Coi a = 3x, b = -y.

${(3x - y)^5} = {\left[ {3x + ( - y)} \right]^5}$

$= {\left( {3x} \right)^5} + 5.{(3x)^4}.( - y) + 10{(3x)^3}.{( - y)^2} + 10{(3x)^2}.{( - y)^3} + 5.(3x).{( - y)^4} + {( - y)^5}$

$= 243{x^5} - 405{x^4}y + 270{x^3}{y^2} - 90{x^2}{y^3} + 15x{y^4} - {y^5}$.

Bài 4:

a) Xác định hệ số của ${x^6}$ trong khai triển ${\left( {2x + 1} \right)^{12}}$.

b) Xác định hệ số của ${x^9}$ trong khai triển ${\left( {3x - 2} \right)^{18}}$.

Giải:

a) Số hạng chứa ${x^6}$ là $C_{12}^6.{\left( {2x} \right)^6} = C_{12}^6{.2^6}{x^6}$. Hệ số của ${x^6}$ là $C_{12}^6{.2^6}$.

b) Số hạng chứa ${x^9}$ là $C_{18}^9.{\left( {3x} \right)^9}.{( - 2)^9} = C_{18}^9.{( - 2)^9}{3^9}{x^9} =  - C_{18}^9{.2^9}{3^9}{x^9}$. Hệ số của ${x^9}$ là $- C_{18}^9{.2^9}{3^9} =  - C_{18}^9{.6^9}$.

Bài 5: Cho tập hợp A = { a; b; c; d; e }. Tập hợp A có bao nhiêu tập hợp con?

Giải:

Tập hợp A có 5 phần tử. Mỗi tập con của A có k phần tử (1 ≤ k ≤ 5) là một tổ hợp chập k của A. Do đó, số tập con như vậy bằng $C_5^k$. Mặt khác, có một tập con của A không có phần tử nào (tập rỗng), tức có $C_5^0 = 1$ tập con như vậy. Do đó, số tập con của A bằng $C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5$.
Theo công thức nhị thức Newton, ta có $C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5 = {(1 + 1)^5} = {2^5}$.

Vậy A có ${2^5} = 32$ tập con.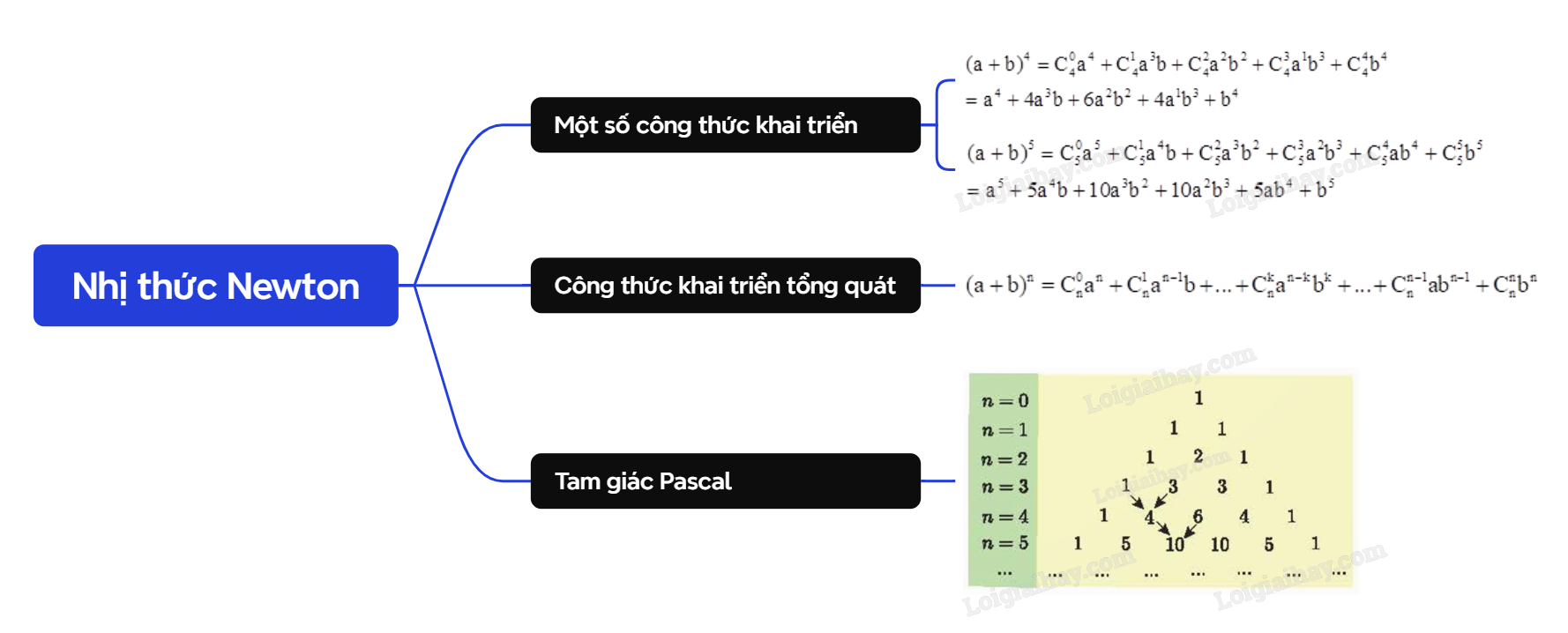