Lý thuyết Hình nón Toán 9 Cánh diều1. Hình nón Định nghĩa Hình nón là hình được tạo ra khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác đó. 1. Hình nón
Định nghĩa
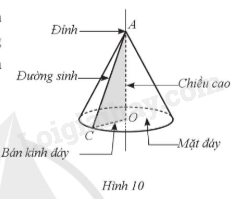
Với hình nón trên, ta có: - Điểm A là đỉnh; - Hình tròn tâm O bán kính OC là mặt đáy; - Độ dài cạnh OC được gọi là bán kính đáy; - Độ dài cạnh AO được gọi là chiều cao; - Cạnh AC quét nên mặt xung quanh của hình nón, mỗi vị trí của cạnh AC được gọi là một đường sinh. Chú ý: Nếu gọi độ dài đường sinh, chiều cao và bán kính đáy của hình nón lần lượt là \(l,h,r\) thì theo định lí Pythagore ta có: \({l^2} = {r^2} + {h^2}\). Ví dụ:
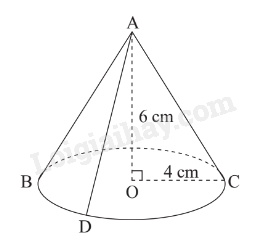
Hình nón có: + A là đỉnh; + chiều cao là 6cm; + bán kính đáy là 4cm. + các đường sinh là: AB, AC, AD. 2. Diện tích xung quanh của hình nón Diện tích xung quanh của hình nón
Diện tích toàn phần của hình nón
Ví dụ:
Diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .6.10 = 60\pi \left( {c{m^2}} \right)\). 3. Thể tích của hình nón
Ví dụ:
Tam giác SOB vuông tại O nên theo định lí Pythagore ta có: \(\begin{array}{l}O{B^2} + S{O^2} = S{B^2}\\{6^2} + S{O^2} = {10^2}\\S{O^2} = 100 - 36 = 64\\SO = 8cm.\end{array}\) Thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \left( {c{m^3}} \right)\).
 Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
