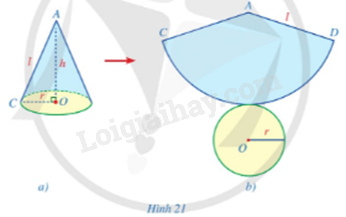
Giải mục 2 trang 100, 101 SGK Toán 9 tập 2 - Cánh diềua) Chuẩn bị một hình nón bằng giấy có bán kính đáy là r, chiều cao là h và độ dài đường sinh là l (Hình 21a); b) Từ hình nón đó, cắt rời đáy và cắt dọc theo đường sinh AC rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình nón là một hình quạt tròn CAD tâm A với bán kính bằng độ dài đường sinh và độ dài cung CD bằng độ dài đường tròn đáy của hình nón (Hình 21b). c) Tính diện tích hình quạt tròn CAD theo r và l. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Lựa chọn câu để xem lời giải nhanh hơn
HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 100 SGK Toán 9 Cánh diều a) Chuẩn bị một hình nón bằng giấy có bán kính đáy là r, chiều cao là h và độ dài đường sinh là l (Hình 21a); b) Từ hình nón đó, cắt rời đáy và cắt dọc theo đường sinh AC rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình nón là một hình quạt tròn CAD tâm A với bán kính bằng độ dài đường sinh và độ dài cung CD bằng độ dài đường tròn đáy của hình nón (Hình 21b). c) Tính diện tích hình quạt tròn CAD theo r và l.
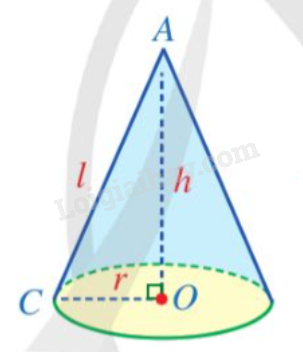
Phương pháp giải: a) Cắt dán một hình nón tùy ý hoặc sử dụng hình có sẵn (mũ sinh nhật,…). b) Làm theo hướng dẫn. c) Diện tích quạt tròn là: Lời giải chi tiết: a) Cắt dán một hình nón tùy ý hoặc sử dụng hình có sẵn (mũ sinh nhật,…). b) Làm theo hướng dẫn. c) Diện tích quạt tròn CAD là: (C là chu vi đáy). Vậy diện tích hình quạt tròn CAD là . LT2 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 2 trang 101 SGK Toán 9 Cánh diều Một chiếc nón lá có dạng hình nón với đường kính đáy khoảng 44 cm, chiều cao khoảng 20 cm. Hỏi diện tích xung quanh của chiếc nón đó bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải: Áp dụng Định lý Pytago để tính độ dài đường sinh: Áp dụng công thức: Lời giải chi tiết:
Chiếc nón lá được biểu diễn dạng hình học như hình bên. Bán kính đáy là:
Đường sinh là: (áp dụng định lý Pytago cho tam giác vuông AOC). Diện tích xung quanh của chiếc nón là:
Vậy diện tích xung quanh của chiếc nón đó là khoảng .
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|