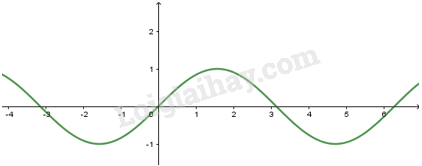
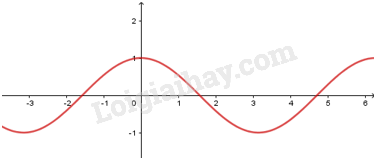
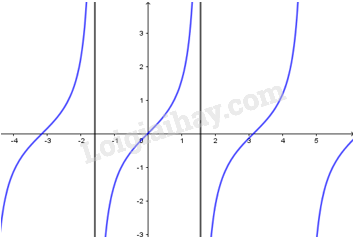
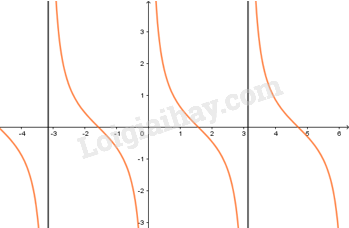
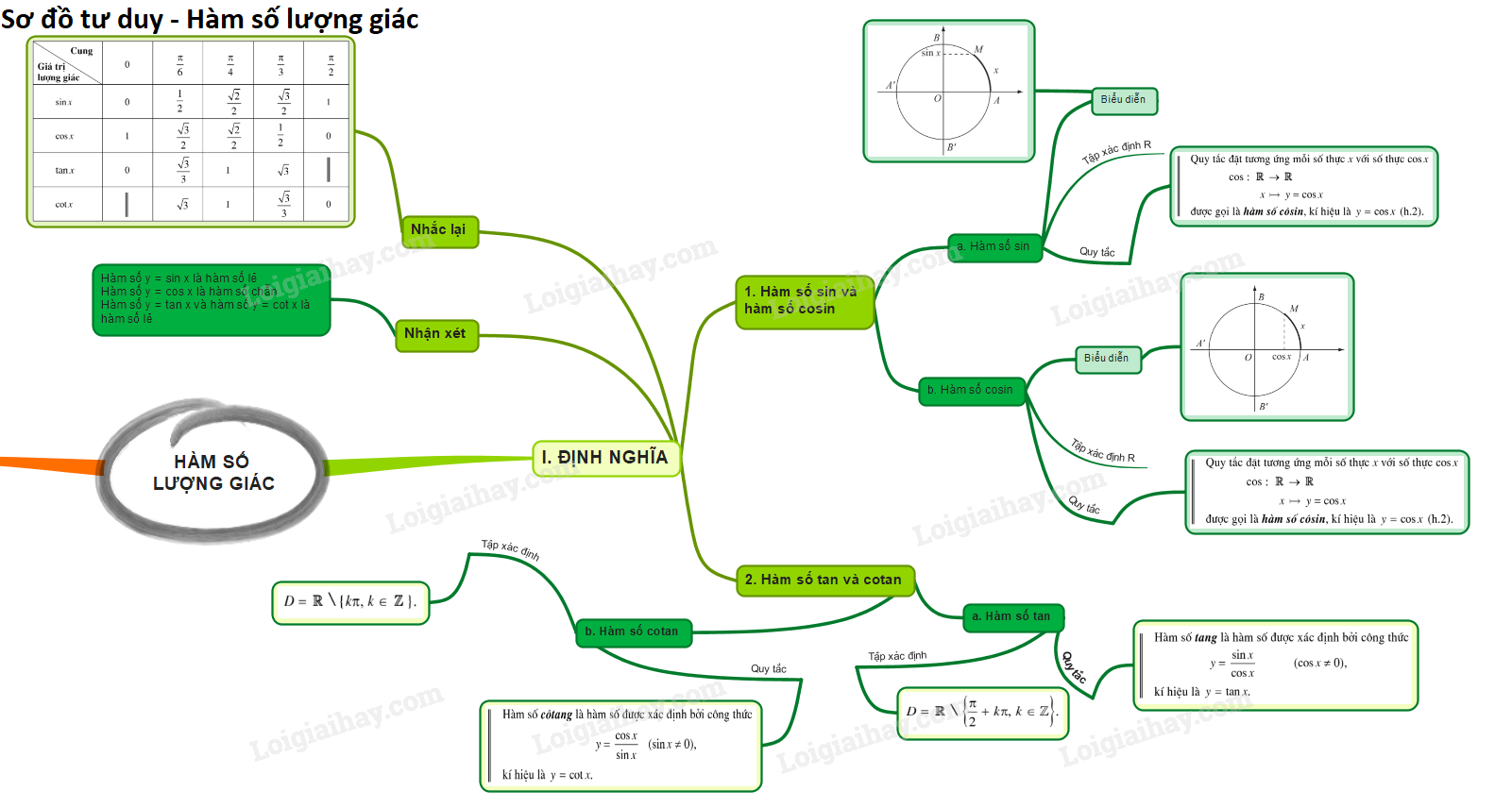
Lý thuyết hàm số lượng giác

1. Hàm số \(y = \sin x\)

- Có TXĐ \(D = R\), là hàm số lẻ, tuần hoàn với chu kì \(2\pi \), nhận mọi giá trị thuộc đoạn \(\left[ { - 1;1} \right]\). 

- Đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k2\pi ;\dfrac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\dfrac{\pi }{2} + k2\pi ;\dfrac{{3\pi }}{2} + k2\pi } \right)\)

- Có đồ thị là đường hình sin đi qua điểm \(O\left( {0;0} \right)\)

2. Hàm số \(y = \cos x\)

- Có TXĐ \(D = R\), là hàm số chẵn, tuần hoàn với chu kì \(2\pi \), nhận mọi giá trị thuộc đoạn \(\left[ { - 1;1} \right]\).

- Đồng biến trên mỗi khoảng \(\left( { - \pi  + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi  + k2\pi } \right)\)

- Có đồ thị là đường hình sin đi qua điểm \(\left( {0;1} \right)\)

3. Hàm số \(y = \tan x\)

- Có TXĐ \(D = R\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}\), là hàm số lẻ, tuần hoàn với chu kì \(\pi \), nhận mọi giá trị thuộc \(R\).

- Đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k\pi ;\dfrac{\pi }{2} + k\pi } \right)\).

4. Hàm số \(y = \cot x\)

- Có TXĐ \(D = R\backslash \left\{ {k\pi ,k \in Z} \right\}\), là hàm số lẻ, tuần hoàn với chu kì \(\pi \), nhận mọi giá trị thuộc \(R\).

- Nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi  + k\pi } \right)\).

HocTot.Nam.Name.Vn