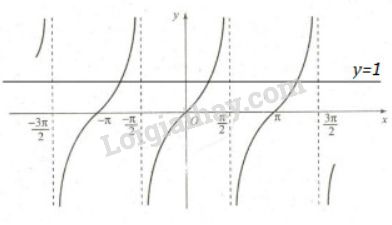
Giải bài 1 trang 17 SGK Đại số và Giải tích 11

LG a

Nhận giá trị bằng \(0\);

Phương pháp giải:

B1: Vẽ đường thẳng y=0 (Ox)

B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=0 tại những điểm nào.

B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.

Lời giải chi tiết:

Trong đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\),

Trục hoành cắt đồ thị hàm số \(y = \tan x\) tại ba điểm có hoành độ \(- π ; 0 ; π\).

Vậy \(x = - π; x = 0 ; x = π\).

LG b

Nhận giá trị bằng \(1\);

Phương pháp giải:

B1: Vẽ đường thẳng y=1 (Ox)

B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=1 tại những điểm nào.

B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.

Lời giải chi tiết:

Đường thẳng \(y = 1\) cắt đồ thị \(y = \tan x\) tại ba điểm có hoành độ \(\displaystyle {\pi  \over 4};{\pi  \over 4} \pm \pi \).

Vậy \(\displaystyle x =  - {{3\pi } \over 4};\,\,x = {\pi  \over 4};\,\,x = {{5\pi } \over 4}\).

LG c

Nhận giá trị dương;

Phương pháp giải:

B1: Quan sát đồ thị hàm số, tìm các giá trị x sao cho đồ thị nằm phía trên trục hoành (hay tanx >0).

B2. Lấy các điểm thuộc đoạn đề bài yêu cầu và Kết luận.

Lời giải chi tiết:

Trong các khoảng \(\displaystyle\left( { - \pi ; - {\pi  \over 2}} \right)\); \(\displaystyle\left( {0;{\pi  \over 2}} \right)\); \(\displaystyle \left( {\pi ;{{3\pi } \over 2}} \right)\), đồ thị hàm số nằm phía trên trục hoành.

Vậy \(\displaystyle x \in \left( { - \pi ; - {\pi  \over 2}} \right) \cup \left( {0;{\pi  \over 2}} \right) \cup \left( {\pi ;{{3\pi } \over 2}} \right)\)

LG d

Nhận giá trị âm.

Phương pháp giải:

Quan sát đồ thị hàm số, tìm các điểm thỏa mãn yêu cầu bài toán.

Lời giải chi tiết:

Trong các khoảng \(\displaystyle\left( { - {\pi  \over 2};0} \right),\left( {{\pi  \over 2};\pi } \right)\), đồ thị hàm số nằm phía dưới trục hoành.

Vậy \(\displaystyle x \in \left( { - {\pi  \over 2};0} \right) \cup \left( {{\pi  \over 2};\pi } \right)\).

HocTot.Nam.Name.Vn