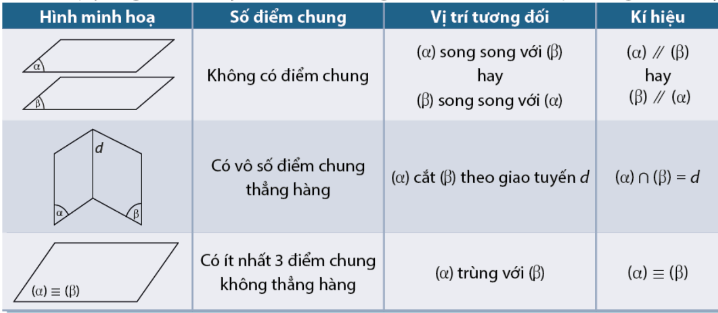
Lý thuyết Hai mặt phẳng song song - SGK Toán 11 Cùng khám pháI. Hai mặt phẳng song song trong không gian I. Hai mặt phẳng song song trong không gian * Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung. *Lưu ý: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( \beta \right)\\d \subset \left( \alpha \right)\end{array} \right. \Rightarrow d//\left( \beta \right)\). II. Tính chất của hai mặt phẳng song song trong không gian
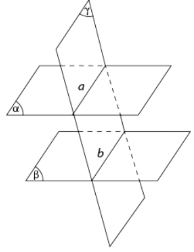
* Hệ quả: - Nếu đường thẳng d song song với \(\left( \alpha \right)\) thì qua d có duy nhất một mặt phẳng song song với \(\left( \alpha \right)\) - Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau. - Cho điểm A không nằm trên mặt phẳng \(\left( \alpha \right)\) .Mọi đường thẳng đi qua A và song song với \(\left( \alpha \right)\)đều nằm trong mặt phẳng đi qua A và song song \(\left( \alpha \right)\).
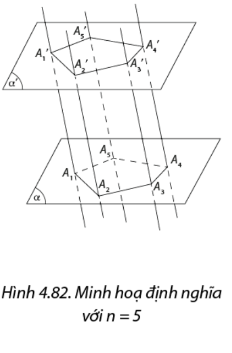
III. Định lí Thalès Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ. \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) IV. Hình lăng trụ và hình hộp - Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha '} \right)\). Trên \(\left( \alpha \right)\) cho đa thức đa giác lồi \({A_1}{A_2}...{A_n}\). Qua các đỉnhvẽ các đường thẳng đôi một song song và cắt mặt phẳng \(\left( {\alpha '} \right)\)tại \({A_1}',{A_2}',...,{A_n}'\). Hình gồm hai đa giác\({A_1}{A_2}...{A_n}\), \({A_1}'{A_2}'...{A_n}'\) và các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\)được gọi là hình lăng trụ và kí hiệu là \({A_1}{A_2}...{A_n}.{A_1}'{A_2}'...{A_n}'\). - Các điểm \({A_1},{A_2},...,{A_n}\) và \({A_1}',{A_2}',...,{A_n}'\)được gọi là các đỉnh, các đoạn thẳng \({A_1}{A_1}',{A_2}{A_2}',...,{A_n}{A_n}'\)được gọi là các cạnh bên, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\)và \({A_1}'{A_2}',{A_2}'{A_3}',...,{A_n}'{A_1}'\) gọi là cạnh đáy của hình trụ. - Hai đa giác \({A_1}{A_2}...{A_n}\)và \({A_1}'{A_2}'...{A_n}'\)được gọi là hai mặt đáy của hình lăng trụ. Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) gọi là các mặt bên của hình trụ. - Hình lăng trụ có đáy là tam giác, tứ giác, ngũ giác,…tương ứng được gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác,… 2.Hình hộp Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
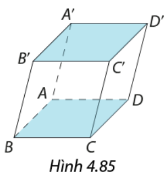
- Trong hình hình hộp có: + Sáu mặt là sau hình bình hành. Mỗi mặt đều có một mặt song song với nó gọi là hai mặt đối diện. + Hai đỉnh không cùng nằm trưn một mặt gọi là hai đỉnh đối diện. + Đoạn thẳng nối 2 đỉnh đối diện gọi là đường chéo. + Bốn đường chéo cắt nhau tại trung điểm mỗi đường. 
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|