Giải mục 2 trang 107, 108, 109, 110 SGK Toán 11 tập 1 - Cùng khám pháCho hai mặt phẳng (α) và (β). Biết rằng hai đường thẳng a và b nằm trong (α) sao cho a//(β) và b//(β).
Lựa chọn câu để xem lời giải nhanh hơn
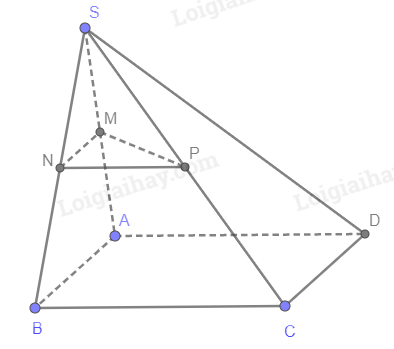
Hoạt động 2 Cho hai mặt phẳng (α) và (β). Biết rằng hai đường thẳng a và b nằm trong (α) sao cho a//(β) và b//(β). a) Vì sao (α) và (β) là hai mặt phẳng phân biệt? b) Nếu (α) cắt (β) theo giao tuyến c thì c có song song với a và b hay không? c) Nếu a cắt b tại M thì (α) và (β) có thể có điểm chung hay không ? Phương pháp giải: a) Hai mặt phẳng phân biệt là hai mặt phẳng không trùng nhau. b) Cho a // (P). Nếu (Q) chứa a và (Q) cắt (P) theo giao tuyến b thì a // b. c) Chứng minh phản chứng (Giả sử (α) và (β) có điểm chung). Lời giải chi tiết: a) Nếu (α) và (β) trùng nhau thì a, b song song với (α) Mà a, b nằm trong (α) (Mâu thuẫn) Vậy (α) và (β) là hai mặt phẳng phân biệt. b) a//(β), b//(β) Mà (α) cắt (β) theo giao tuyến c nên a // c, b // c. c) Giả sử (α) và (β) có điểm chung. Vì (α) cắt (β) là 2 mặt phẳng phân biệt nên (α) cắt (β) Theo phần b, suy ra a // c // b (Mâu thuẫn) Vậy nếu a cắt b tại M thì (α) cắt (β) không có điểm chung. Luyện tập 2 Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABCD). Phương pháp giải: Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q). Lời giải chi tiết:
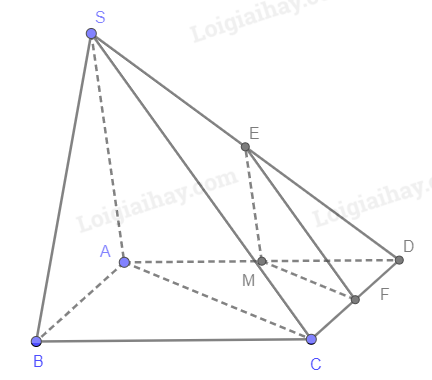
Xét tam giác SAB có M, N lần lượt là trung điểm của SA, SB nên MN // AB. Suy ra MN // (ABCD). Xét tam giác SBC có N, P lần lượt là trung điểm của SB, SC nên NP // BC. Suy ra NP // (ABCD). Vậy (MNP) // (ABCD). Hoạt động 3 Cho điểm A nằm ngoài một mặt phẳng (β). Trong (β), lấy hai đường thẳng cắt nhau a và b. Vẽ các đường thẳng d1, d2 qua A và lần lượt song song với a, b. Gọi (α) là mặt phẳng xác định bởi d1 và d2. Mặt phẳng (α) và (β) có điểm chung không? Vì sao? Phương pháp giải: Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q). Lời giải chi tiết: {d1//aa⊂(β)⇒d1//(β){d2//bb⊂(β)⇒d2//(β) Mặt phẳng (α) chứa d1, d2 cắt nhau tại A và cùng song song với (β) nên (α) song song với (β). Vậy mặt phẳng (α) và (β) không điểm chung. Luyện tập 3 Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Lấy M là trung điểm của đoạn AD. Gọi (α) là mặt phẳng qua M và song song với mặt phẳng (SAC). Xác định giao tuyến của (α) với các mặt của hình chóp đã cho. Phương pháp giải: Kẻ 2 đường thẳng đi qua M và song song với 2 đường thẳng trong (SAC). Lời giải chi tiết:
Trong tam giác SAD, vẽ đường thẳng đi qua M, song song với SA, cắt SD tại E (tức ME là đường trung bình của tam giác SAD), suy ra ME // (SAC) (1). Trong tam giác ACD, vẽ đường thẳng đi qua M, song song với AC, cắt CD tại F (tức MF là đường trung bình của tam giác ACD), suy ra MF // (SAC) (2). Từ (1) và (2) suy ra (ME, MF) // (SAC), do đó (MEF) là (α). (MEF)∩(ABCD)=MF(MEF)∩(SAD)=ME(MEF)∩(SCD)=EF Luyện tập 4 Cho hình chóp S.ABC. Gọi M là trung điểm của SA. Một đường thẳng d đi qua M và song song với mặt phẳng (ABC) nhưng không song song với BC. Xác định giao điểm của d với mặt phẳng (SBC). Phương pháp giải: Kẻ đường thẳng đi qua M và song song với một đường thẳng nằm trong (SBC) khác BC. Lời giải chi tiết:
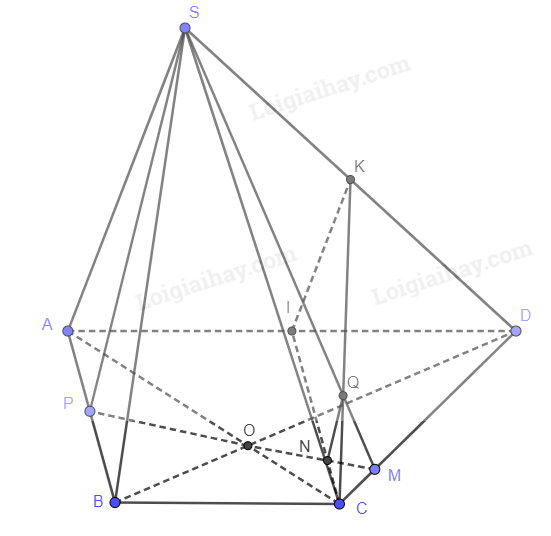
Trong tam giác SAB, vẽ đường thẳng d đi qua M và song song với AB, cắt SB tại D (tức MD là đường trung bình của tam giác SAB), suy ra MD // (ABC). Vậy giao điểm của d với (ABC) là D. Hoạt động 4 Cho mặt phẳng (γ) cắt hai mặt phẳng song song (α) và (β) lần lượt theo hai giao tuyến a và b. Hỏi a và b có điểm chung hay không? Vì sao? Phương pháp giải: Hai đường thẳng lần lượt nằm trong 2 mặt phẳng song song thì song song hoặc chéo nhau. Lời giải chi tiết: Đường thẳng a, b lần lượt nằm trong 2 mặt phẳng (α) và (β) song song với nhau nên a và b song song hoặc chéo nhau. Luyện tập 5 Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn AD = 2BC. Gọi I, K lần lượt là trung điểm của AD và SD. a) Chứng minh rằng (SAB) // (CIK). b) Gọi O là giao điểm của hai đường chéo AC, BD. Lấy M là điểm bất kì trên đoạn CD, đường thẳng OM cắt CI, AB lần lượt tại N, P và SM cắt CK tại Q. Chứng minh rằng SP // NQ. Phương pháp giải: a) Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q). b) Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau. Lời giải chi tiết:
a) Xét tam giác SAD có I, K lần lượt là trung điểm của AD, SD nên IK // SA. Ta có có AD // BC (ABCD là hình thang), AI = BC nên ABCI là hình bình hành. Suy ra IC // AB. Vậy (CIK) // (SAB). b) (SAB)∩(SPM)=SP(CIK)∩(SPM)=NQ Mà (SAB) // (CIK) (cmt) nên SP // NQ.
|