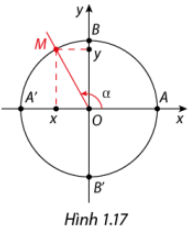
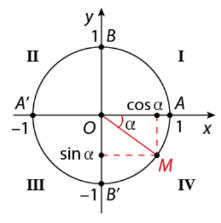
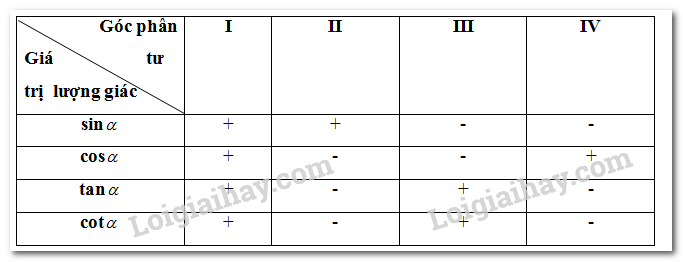
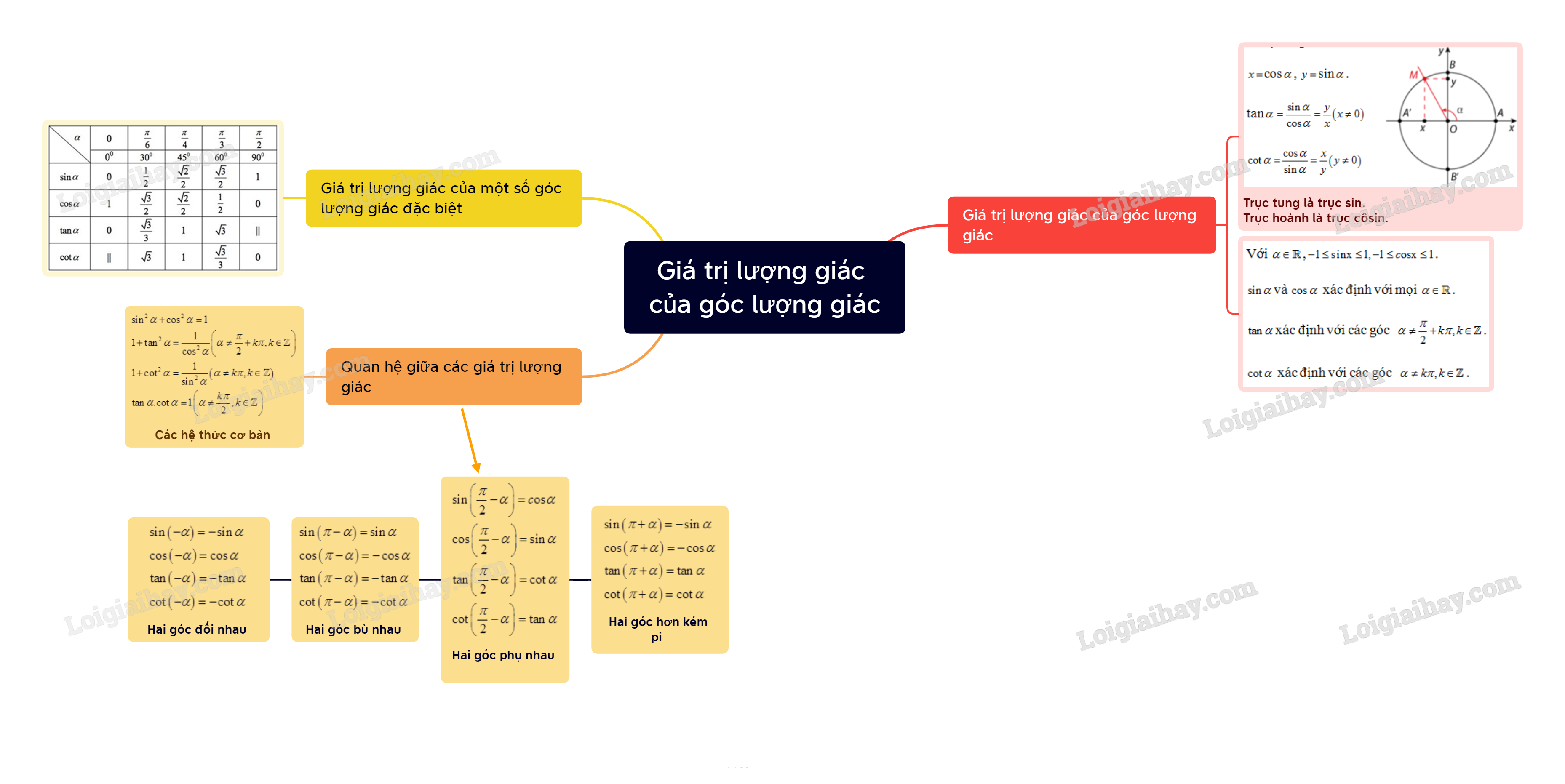
Lý thuyết Giá trị lượng giác của góc lượng giác - SGK Toán 11 Cùng khám phá

I. Giá trị lượng giác của góc lượng giác

1. Định nghĩa

- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:

$x =$cos$\alpha$, $y =$sin$\alpha$.

tan$\alpha$$= \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)$

$\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)$

- Các giá trị sin$\alpha$, cos$\alpha$, tan$\alpha$, cot$\alpha$ được gọi là các giá trị lượng giác của góc lượng giác $\alpha$.

*Chú ý:

a, Trục tung là trục sin, trục hoành là trục côsin.

b, Với $\alpha  \in \mathbb{R}$,$- 1 \le {\mathop{\rm s}\nolimits} {\rm{inx}} \le 1, - 1 \le c{\rm{osx}} \le 1$.

$\sin \alpha$và $\cos \alpha$ xác định với mọi $\alpha  \in \mathbb{R}$.

$\tan \alpha$ xác định với các góc  $\alpha  \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}$.

$\cot \alpha$ xác định với các góc  $\alpha  \ne k\pi ,k \in \mathbb{Z}$.

c, Với mọi góc lượng giác $\alpha$ và số nguyên k, ta có:

$\begin{array}{l}\sin \left( {\alpha  + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha  + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha  + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha  + k\pi } \right) = \cot \alpha \end{array}$

d, Bảng xác định dấu của các giá trị lượng giác

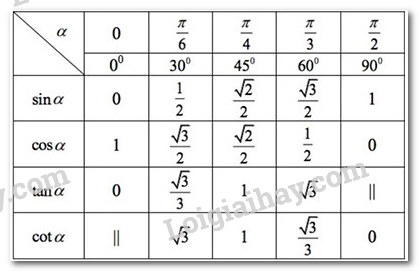
2. Giá trị lượng giác của một số góc lượng giác đặc biệt

3. Sử dụng máy tính cầm tay để tính các giá trị lượng giác của một góc

- Lần lượt ấn các phím SHIFT $\to$MENU $\to$2 (CASIO 580VN)

Để chọn đơn vị độ: ấn phím 1 (Degree).

Để chọn đơn vị radian: ấn phím 2 (Radian).

- Ấn các phím MENU 1 để vào chế độ tính toán.

II. Quan hệ giữa các giá trị lượng giác

1. Các hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác

$\begin{array}{l}{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\\1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha  \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha  \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha  = 1\left( {\alpha  \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}$

2. Quan hệ giữa các giá trị lượng giác của các góc lượng giác có liên quan đặc biệt

• Hai góc đối nhau $\alpha$ và $- \alpha$

$\begin{array}{l}\sin \left( { - \alpha } \right) =  - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) =  - \tan \alpha \\\cot \left( { - \alpha } \right) =  - \cot \alpha \end{array}$

• Hai góc bù nhau ($\alpha$ và $\pi$-$\alpha$)

$\begin{array}{l}\sin \left( {\pi  - \alpha } \right) = \sin \alpha \\\cos \left( {\pi  - \alpha } \right) =  - \cos \alpha \\\tan \left( {\pi  - \alpha } \right) =  - \tan \alpha \\\cot \left( {\pi  - \alpha } \right) =  - \cot \alpha \end{array}$

• Hai góc phụ nhau ($\alpha$ và $\frac{\pi }{2}$-$\alpha$)

$\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}$

• Hai góc hơn kém $\pi$($\alpha$ và $\pi$ + $\alpha$)

$\begin{array}{l}\sin \left( {\pi  + \alpha } \right) =  - \sin \alpha \\\cos \left( {\pi  + \alpha } \right) =  - \cos \alpha \\\tan \left( {\pi  + \alpha } \right) = \tan \alpha \\\cot \left( {\pi  + \alpha } \right) = \cot \alpha \end{array}$