Giải mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1 - Cùng khám phá

Hoạt động 3

a) Từ định nghĩa của \(\sin \alpha \)và \(\cos \alpha \), hãy tính \({\sin ^2}\alpha  + {\cos ^2}\alpha \).

b) Từ định nghĩa của \(\tan \alpha \) và \(\cot \alpha \), hãy tính \(\tan \alpha .\cot \alpha \).

Phương pháp giải:

Lời giải chi tiết:

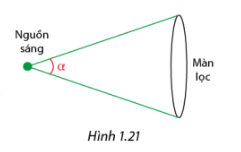
Luyện tập 4

Cường độ ánh sáng I đi xuyên qua một màn lọc ánh sáng được tính bởi công thức \(I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }}\), trong đó I_m là cường độ ánh sáng đã chiếu lên màn lọc ánh sáng và là góc \(\alpha \) như trong Hình 1.21 (nguồn: https://www.vedantu.com/iit-jee/malus-law). Chứng minh rằng: \(I = {I_m}{\cos ^2}\alpha \).

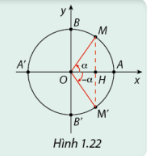
Phương pháp giải:

Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

Lời giải chi tiết:

\(\begin{array}{l}I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }} = {I_m}\left( {1 - \frac{1}{{1 + {{\cot }^2}\alpha }}} \right) = {I_m}.\left( {1 - \frac{1}{{\frac{1}{{{{\sin }^2}\alpha }}}}} \right)\\ = {I_m}.\left( {1 - {{\sin }^2}\alpha } \right) = {I_m}.{\cos ^2}\alpha \end{array}\)

Hoạt động 4

a) Dựa vào Hình 1.22, hãy so sánh \(\cos \left( { - \alpha } \right)\) và \(\cos \left( \alpha  \right)\); \(\sin \left( { - \alpha } \right)\) và \(\sin \left( \alpha  \right)\).

b) Từ đó so sánh \(\tan \left( { - \alpha } \right)\) và \(\tan \left( \alpha  \right)\); \(\cot \left( { - \alpha } \right)\) và \(\cot \left( \alpha  \right)\).

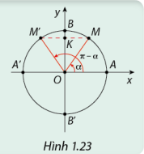
Phương pháp giải:

a) Quan sát hình vẽ.

b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

Lời giải chi tiết:

a) Dựa vào Hình 1.22, ta thấy:

\(\cos \left( { - \alpha } \right)\) = \(\cos \left( \alpha  \right)\)

\(\sin \left( { - \alpha } \right) =  - \sin \left( \alpha  \right)\)

b)

\(\begin{array}{l}\tan \left( { - \alpha } \right) = \frac{{\sin \left( { - \alpha } \right)}}{{\cos \left( { - \alpha } \right)}} = \frac{{ - \sin \alpha }}{{\cos \alpha }} =  - \tan \alpha \\\cot \left( { - \alpha } \right) = \frac{{\cos \left( { - \alpha } \right)}}{{\sin \left( { - \alpha } \right)}} = \frac{{\cos \alpha }}{{ - \sin \alpha }} =  - \cot \alpha \end{array}\)

Hoạt động 5

a) Dựa vào Hình 1.23, hãy so sánh \(\sin \left( {\pi  - \alpha } \right)\) và \(\sin \left( \alpha  \right)\); \(\cos \left( {\pi  - \alpha } \right)\) và \(\cos \left( \alpha  \right)\).

b) Từ đó so sánh \(\tan \left( {\pi  - \alpha } \right)\) và \(\tan \left( \alpha  \right)\); \(\cot \left( {\pi  - \alpha } \right)\) và \(\cot \left( \alpha  \right)\).

Phương pháp giải:

a) Quan sát hình vẽ.

b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

Lời giải chi tiết:

a) Dựa vào Hình 1.23, ta thấy:

\(\sin \left( {\pi  - \alpha } \right)\) = \(\sin \left( \alpha  \right)\)

\(\cos \left( {\pi  - \alpha } \right) =  - \cos \left( \alpha  \right)\)

b) \(\tan \left( {\pi  - \alpha } \right) = \frac{{\sin \left( {\pi  - \alpha } \right)}}{{\cos \left( {\pi  - \alpha } \right)}} = \frac{{\sin \alpha }}{{ - \cos \alpha }} =  - \tan \alpha \)

\(\cot \left( {\pi  - \alpha } \right) = \frac{1}{{\tan \left( {\pi  - \alpha } \right)}} = \frac{1}{{ - \tan \alpha }} =  - \cot \alpha \)

Hoạt động 6

a) Dựa vào Hình 1.24, hãy so sánh \(\sin \left( {\alpha  + \pi } \right)\) và \(\sin \left( \alpha  \right)\); \({\rm{cos}}\left( {\alpha  + \pi } \right)\) và \(\cos \left( \alpha  \right)\).

b) Từ đó so sánh \(\tan \left( {\alpha  + \pi } \right)\) và \(\tan \left( \alpha  \right)\); \(\cot \left( {\alpha  + \pi } \right)\) và \(\cot \left( \alpha  \right)\).

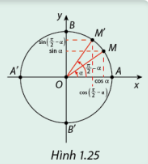
Phương pháp giải:

a) Quan sát hình vẽ.

b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

Lời giải chi tiết:

a) Dựa vào Hình 1.24, ta thấy:

\(\sin \left( {\alpha  + \pi } \right) =  - \sin \alpha \)

\({\rm{cos}}\left( {\alpha  + \pi } \right) =  - \cos \alpha \)

b) \(\tan \left( {\alpha  + \pi } \right) = \frac{{\sin \left( {\alpha  + \pi } \right)}}{{\cos \left( {\alpha  + \pi } \right)}} = \frac{{ - \sin \alpha }}{{ - \cos \alpha }} = \tan \alpha \)

\(\cot \left( {\alpha  + \pi } \right) = \frac{{\cos \left( {\alpha  + \pi } \right)}}{{\sin \left( {\alpha  + \pi } \right)}} = \frac{{ - \cos \alpha }}{{ - \sin \alpha }} = \cot \alpha \)

Hoạt động 7

a) Dựa vào Hình 1.25, hãy so sánh \(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cos \left( \alpha  \right)\); \({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) và \(\sin \left( \alpha  \right)\).

b) Từ đó so sánh \(\tan \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cot \left( \alpha  \right)\); \(\cot \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\tan \left( \alpha  \right)\).

Phương pháp giải:

a) Quan sát hình vẽ.

b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

Lời giải chi tiết:

a) Dựa vào Hình 1.25, ta thấy:

\(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) = \(\cos \left( \alpha  \right)\)

\({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) = \(\sin \left( \alpha  \right)\)

b) \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \cot \alpha \)

\(\cot \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}}{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha \)

Luyện tập 5

Chứng minh giá trị của biểu thức sau không phụ thuộc \(\alpha \):

\(B = {\sin ^2}\left( {\alpha  + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi  - \alpha } \right)\)

Phương pháp giải:

Áp dụng các hệ thức giữa giá trị lượng giác của các góc lượng giác có liên quan đặc biệt.

Lời giải chi tiết:

\(\begin{array}{l}B = {\sin ^2}\left( {\alpha  + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi  - \alpha } \right)\\ \Leftrightarrow B = {\left( { - \sin \alpha } \right)^2} + {\cos ^2}\alpha  + \cos \alpha  - \cos \alpha \\ \Leftrightarrow B = {\sin ^2}\alpha  + {\cos ^2}\alpha \\ \Leftrightarrow B = 1\end{array}\)

Vậy B không phụ thuộc \(\alpha \).