Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức1. Đạo hàm của hàm số tại một điểm Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh 1. Đạo hàm của hàm số tại một điểm - Định nghĩa: Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\). Nếu tồn tại giới hạn (hữu hạn) \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm \({x_0}\), kí hiệu là \(f'\left( {{x_0}} \right)\) hoặc \(y'\left( {{x_0}} \right)\). - Cách viết khác của định nghĩa: \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h}\). - Quy tắc tính đọa hàm của hàm số tại một điểm bằng định nghĩa: Bước 1: Tính \(f\left( x \right) - f\left( {{x_0}} \right)\). Bước 2: Lập và rút gọn tỉ số \(\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) với \(x \in \left( {a;b} \right),x \ne {x_0}\). Bước 3: Tìm giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\). 2. Đạo hàm của hàm số trên một khoảng Hàm số y = f(x) được gọi là đạo hàm trên khoảng (a; b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x). 3. Ý nghĩa hình học của đạo hàm - Hệ số góc tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là \(k = f'\left( {{x_0}} \right)\) nếu đạo hàm \(f'\left( {{x_0}} \right)\) tồn tại. - Phương tình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(M\left( {{x_0};{y_0}} \right)\), \({y_0} = f\left( {{x_0}} \right)\) là: \(y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\). 4. Ý nghĩa vật lí của đạo hàm Vận tốc tức thời của chuyển động s = s(t) tại thời điểm t là v(t) = s’(t). 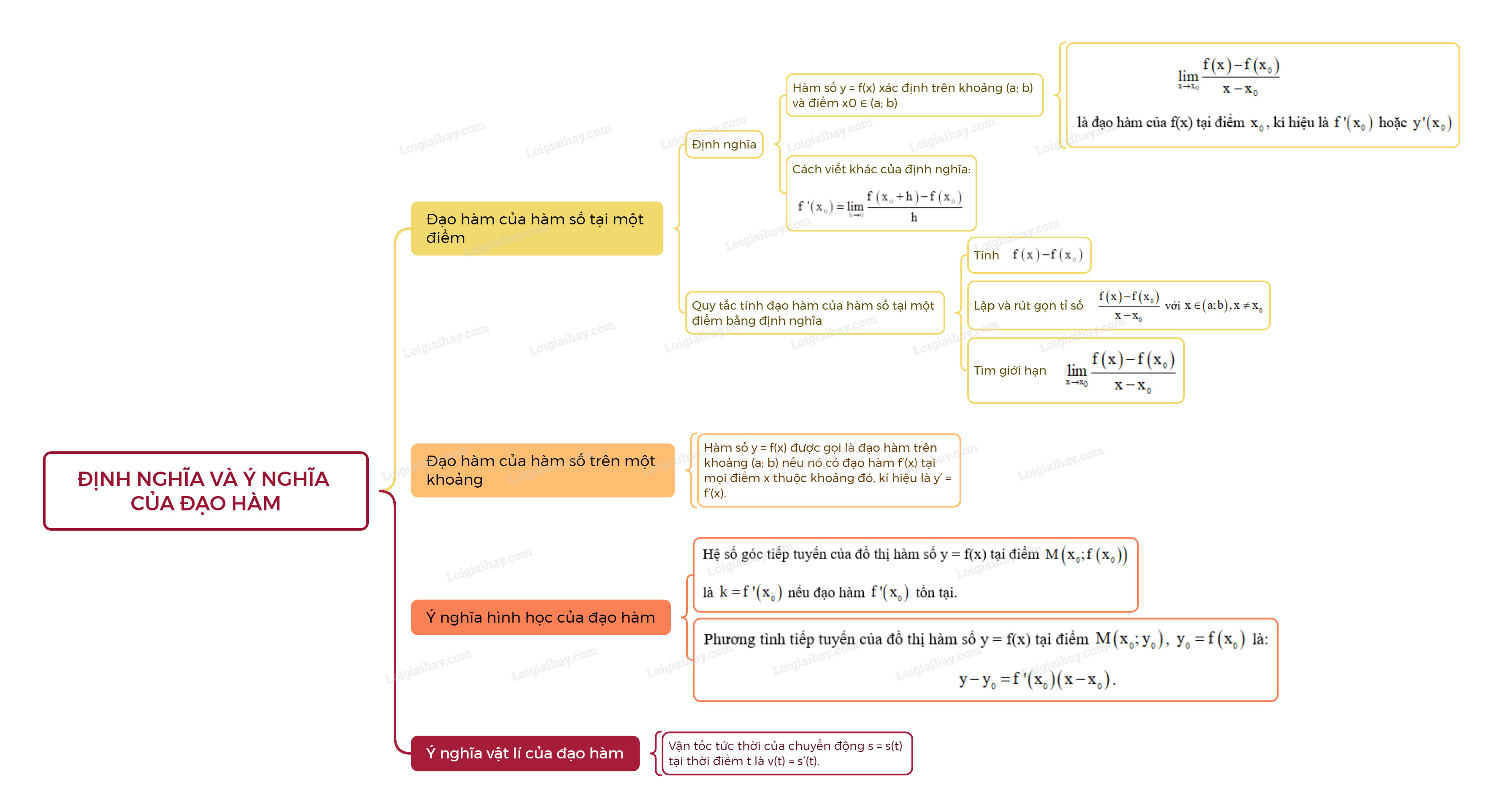
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|





















