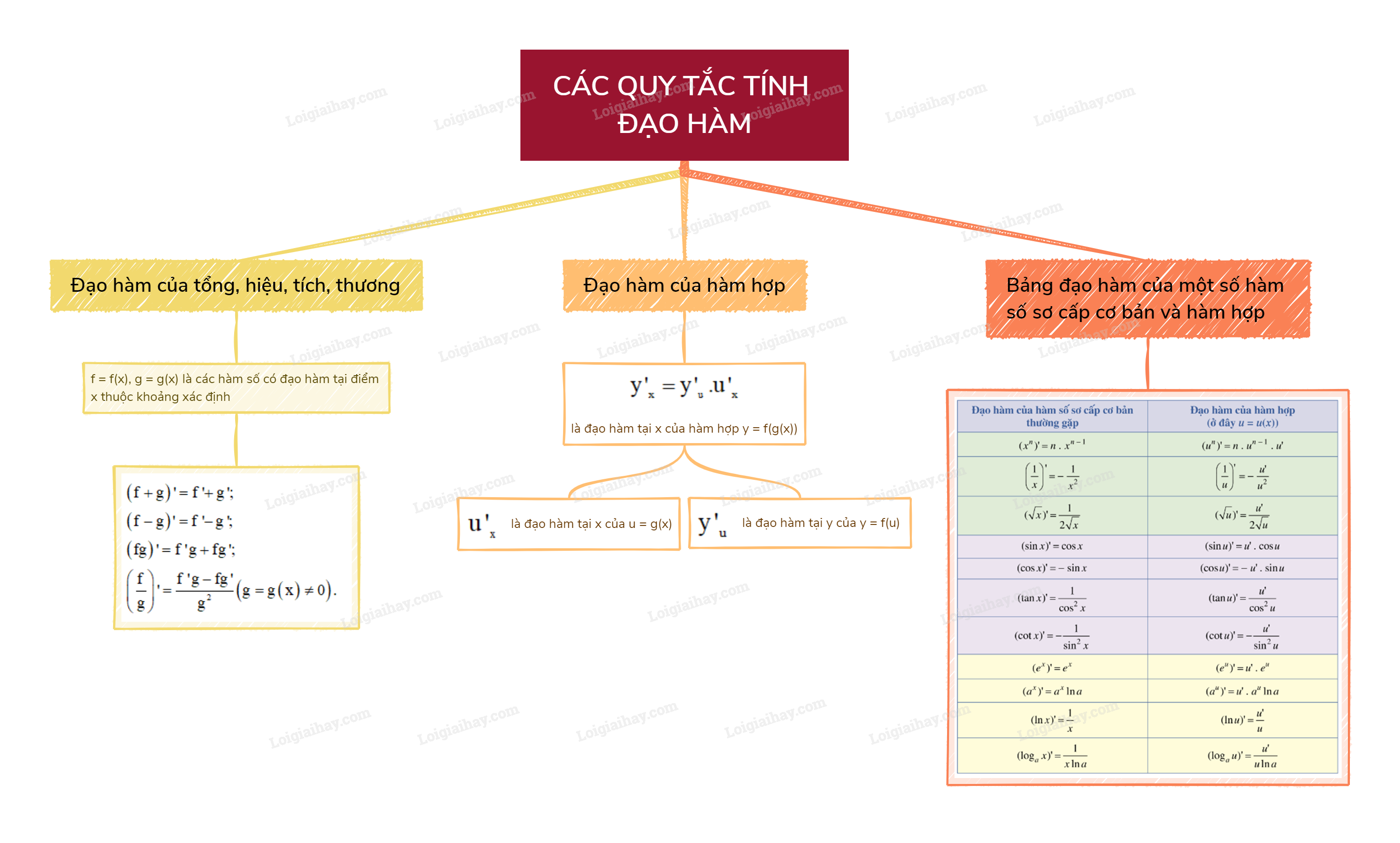
Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Cánh diều1. Đạo hàm của tổng, hiệu, tích, thương Giả sử f = f(x), g = g(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. 1. Đạo hàm của tổng, hiệu, tích, thương Giả sử f = f(x), g = g(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có: \(\begin{array}{l}\left( {f + g} \right)' = f' + g';\\\left( {f - g} \right)' = f' - g';\\\left( {fg} \right)' = f'g + fg';\\\left( {\frac{f}{g}} \right)' = \frac{{f'g - fg'}}{{{g^2}}}\left( {g = g\left( x \right) \ne 0} \right).\end{array}\) 2. Đạo hàm của hàm hợp Nếu hàm số u = g(x) có đạo hàm tại x là \(u{'_x}\) và hàm số y = f(u) có đạo hàm tại y là \(y{'_u}\) thì hàm hợp y = f(g(x)) có đạo hàm tại x là \(y{'_x} = y{'_u}.u{'_x}\). 3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp
 Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
