Giải mục III trang 89, 90 SGK Toán 10 tập 1 - Cánh diều

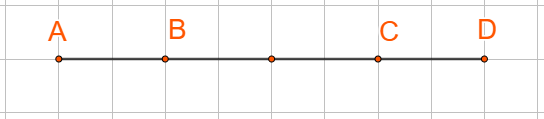
LT-VD 3

Cho tam giác ABC có G là trọng tâm. Chứng minh $\overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG} .$

Phương pháp giải:

G là trọng tâm tam giác ABC thì $\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG}$ với điểm M bất kì.

Lời giải chi tiết:

Với điểm M bất kì ta có: $\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG}$

Chọn M trùng A, ta được: $\overrightarrow {AA}  + \overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG}  \Leftrightarrow \overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG} .$

Hoạt động 6

Cho ba điểm phân biệt A, B, C.

a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto $\overrightarrow {AB} ,\overrightarrow {AC}$ cùng phương hay không?

b) Ngược lại, nếu hai vecto $\overrightarrow {AB} ,\overrightarrow {AC}$ cùng phương thì ba điểm A, B, C có thẳng hàng hay không?

Phương pháp giải:

Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Lời giải chi tiết:

a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto $\overrightarrow {AB} ,\overrightarrow {AC}$ cùng phương.

b) Nếu hai vecto $\overrightarrow {AB} ,\overrightarrow {AC}$ cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.

LT-VD 4

Ở hình 61, tìm k trong mỗi trường hợp sau:

a) $\overrightarrow {AC}  = k.\overrightarrow {AD}$

b) $\overrightarrow {BD}  = k.\overrightarrow {DC}$

Phương pháp giải:

Từ hình vẽ suy ra hướng và tỉ số độ dài của hai vecto.

Lời giải chi tiết:

a) Ta có: $\overrightarrow {AC} ,\overrightarrow {AD}$là hai vecto cùng hướng và $\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|$

Suy ra $\overrightarrow {AC}  = \frac{3}{4}\overrightarrow {AD} .$ Vậy $k = \frac{3}{4}.$

b) Ta có: $\overrightarrow {BD} ,\overrightarrow {DC}$là hai vecto ngược hướng và $\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|$

Suy ra $\overrightarrow {BD}  =  - 3\overrightarrow {DC} .$ Vậy $k =  - 3.$